雷达系统 - 性能因素

影响雷达性能的因素称为雷达性能因素。在本章中，让我们讨论这些因素。我们知道以下标准形式的雷达距离方程，可用于计算给定规格的雷达最大距离。

$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}$$

在哪里，

$P_t$ 是雷达发射的峰值功率

$G$是发射天线的增益

$\sigma$ 是目标的雷达截面

$A_e$是接收天线的有效孔径

$S_{min}$ 是最小可检测信号的功率

从上式中，我们可以得出结论，为了使雷达的射程达到最大，应考虑以下条件。

从雷达距离方程的标准形式很难预测目标的距离。这意味着雷达距离方程提供的关于目标距离的准确度较低。因为，目标的雷达横截面 $\sigma$ 和最小可检测信号 $S_{min}$ 等参数本质上是统计性的。

最小可检测信号

如果回波信号具有最小功率，则雷达检测到该信号被称为最小可检测信号。这意味着，如果回波信号的功率小于最小功率，则雷达无法检测到回波信号。

一般来说，雷达除了接收回波信号外，还接收噪声。如果阈值用于从接收到的信号中检测目标的存在，则该检测称为阈值检测。

我们必须根据待检测信号的强度选择合适的阈值。

下图说明了这个概念 -

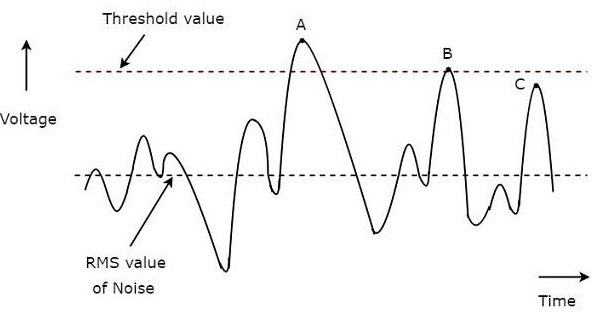
雷达接收器的典型波形如上图所示。x轴和y轴分别表示时间和电压。上图中虚线表示噪声均方根值和阈值。

我们考虑了上图中的 A、B 和 C 三个点来识别有效检测和缺失检测。

因此，点 A 和 B 是有效的检测。而C点是漏检。

如果接收器在接收器接收的信号中产生噪声分量，则这种噪声称为接收器噪声。接收器噪声是不需要的分量；我们应该采取一些预防措施来消除它。

然而，存在一种称为热噪声的噪声。它是由于传导电子的热运动而发生的。从数学上讲，我们可以将接收器产生的热噪声功率$N_i$ 写为 -

$$N_i=KT_oB_n$$

在哪里，

$K$ 是玻尔兹曼常数，等于 $1.38\times 10^{-23}J/deg$

$T_o$ 是绝对温度，等于 $290^0K$

$B_n$ 是接收器带宽

品质因数F只不过是输入 SNR $(SNR)_i$ 与输出 SNR $(SNR)_o$ 的比率。在数学上，它可以表示为 -

$$F=\frac{(SNR)_i}{(SNR)_o}$$

$$\Rightarrow F=\frac{S_i/N_i}{S_o/N_o}$$

$$\Rightarrow F=\frac{N_oS_i}{N_iS_o}$$

$$\右箭头S_i=\frac{FN_iS_o}{N_o}$$

将 $N_i=KT_oB_n$ 代入上式中。

$$\Rightarrow S_i=FKT_oB_n\left ( \frac{S_o}{N_o}\right )$$

当输出信噪比具有最小值时，输入信号功率将具有最小值。

$$\Rightarrow S_{min}=FKT_oB_n\left ( \frac{S_o}{N_o}\right )_{min}$$

将上述$S_{min}$代入以下标准形式的雷达距离方程中。

$$R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 S_{min}}\right ]^{1/4}$$

$$\Rightarrow R_{Max}=\left [\frac{P_tG\sigma A_e}{\left (4\pi\right )^2 FKT_oB_n\left ( \frac{S_o}{N_o}\right )_{min }}\右]^{1/4}$$

从上式中，我们可以得出结论，为了使雷达的射程达到最大，应考虑以下条件。