真分数乘法在线测验建模
以下测验提供与真分数乘法建模相关的多项选择题 (MCQ) 。您必须阅读所有给出的答案并单击正确答案。如果您不确定答案,可以使用“显示答案”按钮检查答案。您可以使用“下一个测验”按钮来检查测验中的新问题集。

答案:A
解释
步骤1:
在这个问题中,我们想要找到$\frac{1}{3}$的$\frac{1}{5}$
第2步:
首先我们将一个矩形的高度分成三等份。我们用阴影表示一部分$\frac{1}{3}$
步骤3:
接下来,我们将宽度分成 5 等份,并遮蔽 1 部分,使其成为$\frac{1}{5}$。
步骤4:
现在我们可以弄清楚产品了。阴影重叠的部分代表分子。零件总数代表分母。共有15个部分,其中1个部分重叠。
第5步:
因此,乘积为$\frac{1}{5}$ × $\frac{1}{3}$ = $\frac{1}{15}$

答案:C
解释
步骤1:
在这个问题中,我们想要找到$\frac{1}{5}$的$\frac{1}{4}$
第2步:
首先我们将一个长方形的高度分成4等份。我们用阴影表示一部分$\frac{1}{4}$
步骤3:
接下来,我们将宽度分成 5 等份,并遮蔽 1 部分,使其成为$\frac{1}{5}$。
步骤4:
现在我们可以弄清楚产品了。阴影重叠的部分代表分子。零件总数代表分母。总共有20个部分,其中有一个部分是重叠的。
第5步:
因此,乘积为$\frac{1}{5}$ × $\frac{1}{4}$ = $\frac{1}{20}$

答案:B
解释
步骤1:
在这个问题中,我们想要找到$\frac{1}{5}$的$\frac{1}{6}$
第2步:
首先我们将一个长方形的高度分成6等份。我们用阴影表示一部分$\frac{1}{6}$
步骤3:
接下来,我们将宽度分成 5 等份,并遮蔽 1 部分,使其成为$\frac{1}{5}$。
步骤4:
现在我们可以弄清楚产品了。阴影重叠的部分代表分子。零件总数代表分母。共有 30 个相等的部分,其中一个部分重叠。
第5步:
因此,乘积为$\frac{1}{5}$ × $\frac{1}{6}$ = $\frac{1}{30}$
答案:D
解释
步骤1:
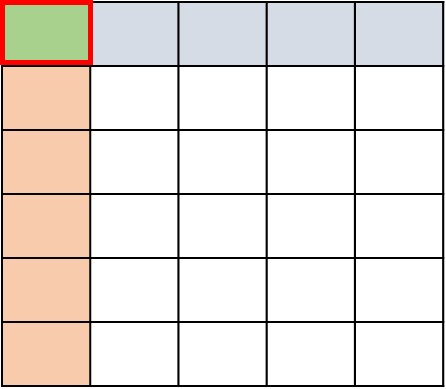
在这个问题中,我们想要找到$\frac{1}{2}$的$\frac{1}{4}$
第2步:
首先我们将一个长方形的高度分成4等份。我们用阴影表示一部分$\frac{1}{4}$
步骤3:
接下来,我们将宽度分成 2 个相等的部分,并对 1 部分进行着色,使其成为$\frac{1}{2}$。
步骤4:
现在我们可以弄清楚产品了。阴影重叠的部分代表分子。零件总数代表分母。共有8部分,其中1部分是重叠的。
第5步:
因此,乘积为$\frac{1}{2}$ × $\frac{1}{4}$ = $\frac{1}{8}$

答案:C
解释
步骤1:
在这个问题中,我们想要找到$\frac{2}{5}$ 的$\frac{1}{2}$
第2步:
首先,我们将矩形的高度分成两等份。我们用阴影表示一部分$\frac{1}{2}$。
步骤3:
接下来,我们将宽度分成 5 个相等的部分,并对 2 个部分进行阴影处理,使其成为$\frac{2}{5}$。
步骤4:
现在我们可以弄清楚产品了。阴影重叠的部分代表分子。零件总数代表分母。总共有 10 个部分,其中两个部分重叠。
第5步:
因此,乘积为$\frac{2}{5}$ × $\frac{1}{2}$ = $\frac{2}{10}$

答案:A
解释
步骤1:
在这个问题中,我们想要找到$\frac{1}{2}$的$\frac{2}{3}$
第2步:
首先,我们将矩形的高度分成两等份。我们用阴影表示一部分$\frac{1}{2}$。
步骤3:
接下来,我们将宽度分为 3 个相等的部分,并对 2 个部分进行阴影处理,使其成为$\frac{2}{3}$。
步骤4:
现在我们可以弄清楚产品了。阴影重叠的部分代表分子。零件总数代表分母。总共有6个部分,其中两个部分重叠。
第5步:
因此,乘积为$\frac{2}{3}$ × $\frac{1}{2}$ = $\frac{2}{6}$

答案:B
解释
步骤1:
在这个问题中,我们想要找到$\frac{1}{2}$的$\frac{1}{2}$
第2步:
首先,我们将矩形的高度分成两等份。我们用阴影表示一部分$\frac{1}{2}$
步骤3:
接下来,我们将宽度分成 2 个相等的部分,并对 1 部分进行着色,使其成为$\frac{1}{2}$。
步骤4:
现在我们可以弄清楚产品了。阴影重叠的部分代表分子。零件总数代表分母。总共有 4 个部分,其中有一个部分是重叠的。
第5步:
因此,乘积为$\frac{1}{2}$ × $\frac{1}{2}$ = $\frac{1}{4}$

答案:D
解释
步骤1:
在这个问题中,我们想要找到$\frac{1}{6}$的$\frac{2}{3}$
第2步:
首先我们将一个长方形的高度分成6等份。我们用阴影表示一部分$\frac{1}{6}$
步骤3:
接下来,我们将宽度分为 3 个相等的部分,并对 2 个部分进行阴影处理,使其成为$\frac{2}{3}$。
步骤4:
现在我们可以弄清楚产品了。阴影重叠的部分代表分子。零件总数代表分母。共有18个部分,其中两个部分重叠。
第5步:
因此,乘积为$\frac{2}{3}$ × $\frac{1}{6}$ = $\frac{2}{18}$

答案:B
解释
步骤1:
在这个问题中,我们想要找到$\frac{3}{4}$的$\frac{1}{2}$
第2步:
首先,我们将矩形的高度分成两等份。我们用阴影表示一部分$\frac{1}{2}$
步骤3:
接下来,我们将宽度分为 4 个相等的部分,并对 3 个部分进行阴影处理,使其成为$\frac{3}{4}$。
步骤4:
现在我们可以弄清楚产品了。阴影重叠的部分代表分子。零件总数代表分母。共有8个部分,其中三个部分重叠。
第5步:
因此,乘积为$\frac{3}{4}$ × $\frac{1}{2}$ = $\frac{3}{8}$

答案:C
解释
步骤1:
在这个问题中,我们想要找到$\frac{1}{6}$的$\frac{1}{2}$
第2步:
首先我们将一个长方形的高度分成6等份。我们用阴影表示一部分$\frac{1}{6}$
步骤3:
接下来,我们将宽度分成 2 个相等的部分,并对 1 部分进行着色,使其成为$\frac{1}{2}$。
步骤4:
现在我们可以弄清楚产品了。阴影重叠的部分代表分子。零件总数代表分母。共有12部分,其中1部分是重叠的。
第5步:
因此,乘积为$\frac{1}{2}$ × $\frac{1}{6}$ = $\frac{1}{12}$

