自适应模糊控制器
在本章中,我们将讨论什么是自适应模糊控制器及其工作原理。自适应模糊控制器设计有一些可调参数以及用于调整它们的嵌入式机制。自适应控制器被用来提高控制器的性能。
实现自适应算法的基本步骤
现在让我们讨论实现自适应算法的基本步骤。
可观察数据的收集- 收集可观察数据以计算控制器的性能。
控制器参数的调整- 现在,借助控制器性能,可以完成控制器参数调整的计算。
控制器性能的改进- 在此步骤中,调整控制器参数以提高控制器的性能。
经营理念
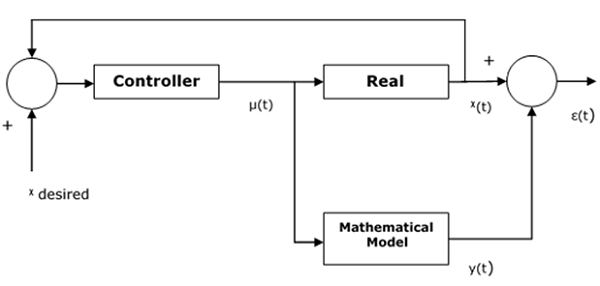
控制器的设计基于类似于真实系统的假设数学模型。计算实际系统与其数学表示之间的误差,如果误差相对较小,则假设模型有效工作。
还存在为控制器的有效性设置边界的阈值常数。控制输入被馈送到实际系统和数学模型中。这里,假设$x\left ( t \right )$ 是真实系统的输出,$y\left ( t \right )$ 是数学模型的输出。那么误差 $\epsilon \left ( t \right )$ 可以计算如下 -
$$\epsilon \left ( t \right ) = x\left ( t \right ) - y\left ( t \right )$$
这里,$x$desired是我们想要从系统中得到的输出,而$\mu\left(t\right)$是来自控制器并进入真实模型和数学模型的输出。
下图显示了如何在实际系统的输出和数学模型之间跟踪误差函数 -
系统参数化
基于模糊数学模型设计的模糊控制器将具有以下形式的模糊规则 -
规则 1 − IF $x_1\left ( t_n \right )\in X_{11} \: AND...AND\: x_i\left ( t_n \right )\in X_{1i}$
那么 $\mu _1\left ( t_n \right ) = K_{11}x_1\left ( t_n \right ) + K_{12}x_2\left ( t_n \right ) \: +...+ \: K_{1i }x_i\左 ( t_n \右 )$
规则 2 − IF $x_1\left ( t_n \right )\in X_{21} \: AND...AND \: x_i\left ( t_n \right )\in X_{2i}$
那么 $\mu _2\left ( t_n \right ) = K_{21}x_1\left ( t_n \right ) + K_{22}x_2\left ( t_n \right ) \: +...+ \: K_{2i }x_i\左 ( t_n \右 ) $
。
。
。
规则 j − IF $x_1\left ( t_n \right )\in X_{k1} \: AND...AND \: x_i\left ( t_n \right )\in X_{ki}$
那么 $\mu _j\left ( t_n \right ) = K_{j1}x_1\left ( t_n \right ) + K_{j2}x_2\left ( t_n \right ) \: +...+ \: K_{ji }x_i\左 ( t_n \右 ) $
上述参数组表征了控制器。
机制调整
调整控制器参数以提高控制器的性能。计算调整参数的过程就是调整机制。
从数学上讲,令 $\theta ^\left ( n \right )$ 为在 $t = t_n$ 时刻调整的一组参数。调整可以是参数的重新计算,
$$\theta ^\left ( n \right ) = \Theta \left ( D_0,\: D_1, \: ..., \:D_n \right )$$
这里 $D_n$ 是在时间 $t = t_n$ 时收集的数据。
现在,通过根据其先前值更新参数集来重新制定该公式,如下所示:
$$\theta ^\left ( n \right ) = \phi ( \theta ^{n-1}, \: D_n)$$
选择自适应模糊控制器的参数
选择自适应模糊控制器需要考虑以下参数 -
系统可以完全用模糊模型来近似吗?
如果一个系统可以完全用模糊模型来近似,那么这个模糊模型的参数是容易获得的还是必须在线确定?
如果一个系统不能完全用模糊模型来近似,是否可以用一组模糊模型来分段近似?
如果一个系统可以用一组模糊模型来近似,那么这些模型是否具有相同的格式但具有不同的参数,还是具有不同的格式?
如果一个系统可以通过一组具有相同格式的模糊模型来近似,每个模糊模型具有不同的参数集,那么这些参数集是容易获得的还是必须在线确定?
