模糊逻辑 - 集合论
模糊集可以被认为是经典集的扩展和总体过度简化。在集合成员资格的背景下可以最好地理解它。基本上它允许部分成员资格,这意味着它包含在集合中具有不同程度的成员资格的元素。由此,我们可以理解经典集合和模糊集合的区别。经典集合包含满足精确隶属属性的元素,而模糊集合包含满足不精确隶属属性的元素。
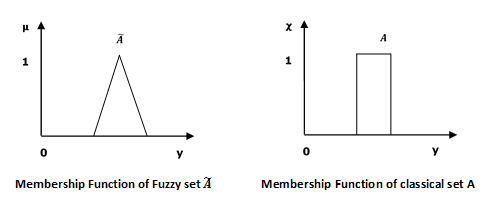
数学概念
信息域 $U$ 中的模糊集 $\widetilde{A}$ 可以定义为一组有序对,并且可以在数学上表示为 -
$$\widetilde{A} = \left \{ \left ( y,\mu _{\widetilde{A}} \left ( y \right ) \right ) | y\in U\right \}$$
这里 $\mu _{\widetilde{A}}\left ( y \right )$ = $y$ 在 \widetilde{A} 中的隶属度,假设值在 0 到 1 的范围内,即 $\mu _{\widetilde{A}}(y)\in \left [ 0,1 \right ]$。
模糊集的表示
现在让我们考虑信息域的两种情况,并了解如何表示模糊集。
情况1
当信息域 $U$ 是离散且有限的时 -
$$\widetilde{A} = \left \{ \frac{\mu _{\widetilde{A}}\left ( y_1 \right )}{y_1} +\frac{\mu _{\widetilde{A}} \left ( y_2 \right )}{y_2} +\frac{\mu _{\widetilde{A}}\left ( y_3 \right )}{y_3} +...\right \}$$
$= \left \{ \sum_{i=1}^{n}\frac{\mu _{\widetilde{A}}\left ( y_i \right )}{y_i} \right \}$
案例2
当信息宇宙 $U$ 是连续且无限时 -
$$\widetilde{A} = \left \{ \int \frac{\mu _{\widetilde{A}}\left ( y \right )}{y} \right \}$$
在上面的表示中,求和符号表示每个元素的集合。
模糊集的运算
有两个模糊集 $\widetilde{A}$ 和 $\widetilde{B}$、信息域 $U$ 和一个元素
