模拟通信 - DSBSC 调制

---

在幅度调制过程中，调制波由载波和两个边带组成。调制波仅在边带中具有信息。边带不过是包含功率的频带，即载波频率的较低频率和较高频率。

包含一个载波和两个边带的信号传输可称为双边带全载波系统或简称DSBFC。其绘制如下图所示。

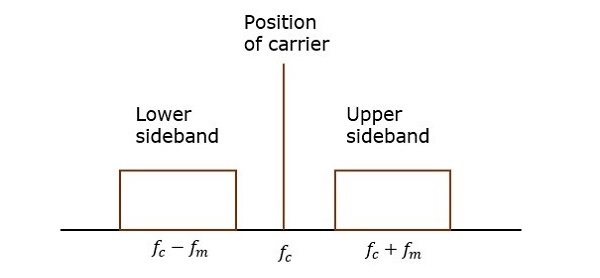
然而，这样的传输效率低下。因为，三分之二的电力都浪费在了载体上，载体上不携带任何信息。

如果该载波被抑制并且节省的功率被分配到两个边带，则这样的过程被称为双边带抑制载波系统或简称为DSBSC。其绘制如下图所示。

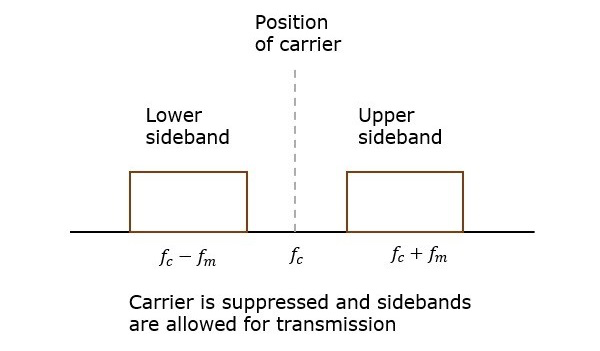
数学表达式

让我们考虑与我们在前面的章节中考虑过的相同的调制和载波信号的数学表达式。

即调制信号

$$m\left ( t \right )=A_m \cos \left ( 2 \pi f_mt\right )$$

载波信号

$$c\left ( t \right )=A_c \cos \left ( 2 \pi f_ct\right )$$

在数学上，我们可以将DSBSC 波的方程表示为调制信号和载波信号的乘积。

$$s\left ( t \right )=m\left ( t \right )c\left ( t \right )$$

$$\Rightarrow s\left ( t \right )=A_mA_c \cos \left ( 2 \pi f_mt \right )\cos \left ( 2 \pi f_ct \right )$$

DSBSC波的带宽

我们知道带宽（BW）的公式是

$$BW=f_{最大值}-f_{最小值}$$

考虑 DSBSC 调制波的方程。

$$s\left ( t \right )=A_mA_c \cos\left ( 2 \pi f_mt \right ) \cos(2 \pi f_ct)$$

$$\Rightarrow s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right ) t\right ]+\frac{A_mA_c}{2 } \cos\left [ 2 \pi\left ( f_c-f_m \right ) t\right ]$$

DSBSC 调制波只有两个频率。因此，最大和最小频率分别为 $f_c+f_m$ 和 $f_c-f_m$。

IE，

$f_{max}=f_c+f_m$ 和 $f_{min}=f_c-f_m$

将 $f_{max}$ 和 $f_{min}$ 值代入带宽公式中。

$$BW=f_c+f_m-\左 (f_c-f_m \右)$$

$$\右箭头 BW=2f_m$$

因此，DSBSC波的带宽与AM波的带宽相同，等于调制信号频率的两倍。

DSBSC 波的功率计算

考虑以下 DSBSC 调制波方程。

$$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c+f_m \right ) t\right ]+\frac{A_mA_c}{2} \ cos\left [ 2 \pi \left ( f_c-f_m \right ) t\right ]$$

DSBSC波的功率等于上边带和下边带频率分量的功率之和。

$$P_t=P_{USB}+P_{LSB}$$

我们知道cos信号功率的标准公式是

$$P=\frac{{v_{rms}}^{2}}{R}=\frac{\left ( v_m\sqrt{2}\right )^2}{R}$$

首先，我们来一一求一下上边带和下边带的功率。

上边带功率

$$P_{USB}=\frac{\left ( A_mA_c / 2\sqrt{2}\right )^2}{R}=\frac{{A_{m}}^{2}{A_{c}} ^{2}}{8R}$$

类似地，我们将得到与上边带功率相同的下边带功率。

$$P_{USB}=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$

现在，让我们将这两个边带功率相加，以获得 DSBSC 波的功率。

$$P_t=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}+\frac{{A_{m}}^{2}{A_{c} }^{2}}{8R}$$

$$\Rightarrow P_t=\frac{{A_{m}}^{2}{A_{c}}^{2}}{4R}$$

因此，发射DSBSC波所需的功率等于两个边带的功率。