模拟通信 - SNR 计算
在本章中,我们将计算在接收机处解调的各种调制波的信噪比和品质因数。
信噪比
信噪比 (SNR)是信号功率与噪声功率之比。SNR 值越高,接收输出的质量就越高。
不同点的信噪比可以使用以下公式计算。
输入 SNR = $\left ( SNR \right )_I= \frac{调制信号的平均功率}{调制信号的平均功率\:\:输入\:\:噪声}$
输出 SNR = $\left ( SNR \right )_O= \frac{解调信号的平均功率}{平均功率\:\:输出\:\:噪声}$
通道 SNR = $\left ( SNR \right )_C= \frac{调制信号的平均功率}{调制信号的平均功率\:\:消息\:\:噪声\:\:带宽}$
品质因数
输出信噪比和输入信噪比的比率可以称为品质因数。它由F表示。它描述了设备的性能。
$$F=\frac {\left ( SNR \right )_O}{\left ( SNR \right )_I}$$
接收器的品质因数是
$$F=\frac {\left ( SNR \right )_O}{\left ( SNR \right )_C}$$
之所以如此,是因为对于接收器来说,通道就是输入。
AM 系统中的 SNR 计算
考虑以下 AM 系统的接收器模型来分析噪声。
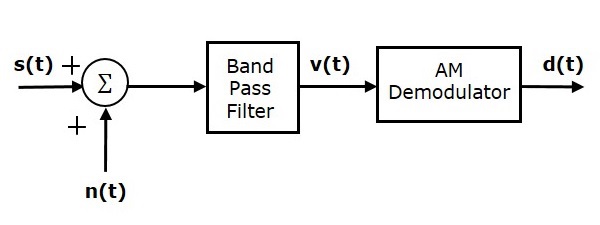
我们知道调幅(AM)波是
$$s\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
$$\Rightarrow s\left ( t \right )=A_c \cos \left ( 2 \pi f_ct \right )+A_ck_am\left ( t \right ) \cos\left ( 2 \pi f_ct \right )$$
AM波的平均功率为
$$P_s=\left ( \frac{A_c}{\sqrt{2}} \right )^2+\left ( \frac{A_ck_am\left ( t \right )}{\sqrt{2}} \right ) ^2=\frac{{A_{c}}^{2}}{2}+\frac{{A_{c}}^{2}{k_{a}}^{2}P}{2}$ $
$$\Rightarrow P_s=\frac{{A_{c}}^{2}\left ( 1+{k_{a}}^{2}P \right )}{2}$$
消息带宽中的平均噪声功率为
$$P_{nc}=WN_0$$
将这些值代入信道SNR公式中
$$\left ( SNR \right )_{C,AM}=\frac{\:\: AM \:\: 的平均 \:\: 功率 \:\: 波}{平均 \:\: 功率 \: \: 的\:\: 噪声\:\: 在\:\: 消息\:\: 带宽}$$
$$\Rightarrow \left ( SNR \right )_{C,AM}=\frac{{A_{c}}^{2}\left ( 1+ {k_{a}}^{2}\right )P {2WN_0}$$
在哪里,
P是消息信号的功率=$\frac{{A_{m}}^{2}}{2}$
W是消息带宽
假设带通噪声在通道中与 AM 波混合,如上图所示。该组合应用于 AM 解调器的输入。因此,AM解调器的输入为。
$$v\left ( t \right )=s\left ( t \right )+n\left ( t \right )$$
$\Rightarrow v\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )+$
$\left [ n_1\left ( t \right ) \cos\left ( 2 \pi f_ct \right ) - n_Q\left ( t \right ) \sin \left ( 2 \pi f_ct \right )\right ]$
$\Rightarrow v\left ( t \right )=\left [ A_c+A_ck_am\left ( t \right )+n_1\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )- n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right )$
其中 $n_I \left ( t \right )$ 和 $n_Q \left ( t \right )$ 是噪声的同相和正交相位分量。
AM解调器的输出只不过是上述信号的包络。
$$d\left ( t \right )=\sqrt{\left [ A_c+A_cK_am\left ( t \right )+n_I\left ( t \right ) \right ]^2+\left ( n_Q\left ( t \右)\右)^2}$$
$$\Rightarrow d\left ( t \right )\大约 A_c+A_ck_am\left ( t \right )+n_1\left ( t \right )$$
解调信号的平均功率为
$$P_m=\left ( \frac{A_ck_am\left ( t \right )}{\sqrt{2}} \right )^2=\frac{{A_{c}}^{2}{k_{a} }^{2}P}{2}$$
输出端噪声的平均功率为
$$P_no=WN_0$$
将这些值代入输出 SNR公式中。
$$\left ( SNR \right )_{O,AM}= \frac {\:\: 解调信号 \:\: 的平均 \:\: 功率 \:\: {平均 \:\: 功率 \: \: 的 \:\: 噪音 \:\: 在 \:\: 输出}$$
$$\Rightarrow \left (信噪比\right)_{O,AM}=\frac{{A_{c}}^{2}{k_{a}}^{2}P}{2WN_0}$$
代入AM 接收机品质因数公式中的值。
$$F=\frac{\left ( SNR \right )_{O,AM}}{\left ( SNR \right )_{C,AM}}$$
$$\Rightarrow F=\left ( \frac{{A_{c}^{2}}{k_{a}^{2}}P}{2WN_0} \right )/\left ( \frac{{A_{ c}}^{2}\left ( 1+ {k_{a}}^{2}\right )P}{2WN_0} \right )$$
$$\Rightarrow F=\frac{{K_{a}}^{2}P}{1+{K_{a}}^{2}P}$$
因此,AM接收器的品质因数小于1。
DSBSC 系统中的 SNR 计算
考虑以下 DSBSC 系统的接收器模型来分析噪声。
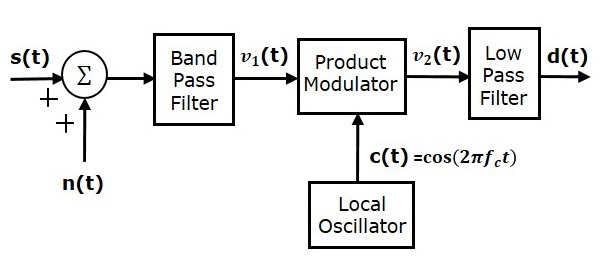
我们知道 DSBSC 调制波是
$$s\left ( t \right )=A_cm\left ( t \right ) \cos\left ( 2 \pi f_ct \right )$$
DSBSC调制波的平均功率为
$$P_s=\left ( \frac{A_cm\left ( t \right )}{\sqrt{2}} \right )^2=\frac{{A_{c}}^{2}P}{2} $$
消息带宽中的平均噪声功率为
$$P_{nc}=WN_0$$
将这些值代入信道 SNR公式中。
$$\left ( SNR \right )_{C,DSBSC}=\frac{\:\: DSBSC \:\: 调制波的平均 \:\: 功率 \:\: {平均 \: \:\: 消息\:\: 中\:\: 噪声\:\: 的功率\:\: 带宽}$$
$$\Rightarrow \left ( SNR \right )_{C,DSBSC}=\frac{{A_{c}}^{2}P}{2WN_0}$$
假设带通噪声与 DSSBSC 调制波在通道中混合,如上图所示。该组合用作乘积调制器的输入之一。因此,该乘积调制器的输入是
$$v_1\left ( t \right )=s\left ( t \right )+n\left ( t \right )$$
$$\Rightarrow v_1\left ( t \right )=A_cm\left ( t \right ) \cos \left ( 2 \pi f_ct \right )+\left [ n_I\left ( t \right ) \cos\left ( 2 \pi f_ct \right ) - n_Q\left ( t \right ) \sin \left ( 2 \pi f_ct \right )\right ]$$
$$\Rightarrow v_1\left ( t \right )=\left [ A_cm \left ( t \right ) +n_I\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )-n_Q \left ( t \right ) \sin\left ( 2 \pi f_ct \right )$$
本地振荡器生成载波信号$c\left ( t \right )= \cos\left ( 2 \pi f_ct \right )$。该信号用作乘积调制器的另一个输入。因此,乘积调制器产生一个输出,它是 $v_1\left ( t \right )$ 和 $c\left ( t \right )$ 的乘积。
$$v_2\left ( t \right )= v_1\left ( t \right )c\left ( t \right )$$
将 $v_1\left ( t \right )$ 和 $c\left ( t \right )$ 值代入上述方程中。
$$\Rightarrow v_2\left ( t \right )=\left ( \left [ A_cm\left ( t \right ) + n_I\left ( t \right )\right ] \cos\left ( 2 \pi f_ct \right )- n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right ) \right ) \cos\left ( 2 \pi f_ct \right )$$
$$\Rightarrow v_2\left ( t \right )=\left [ A_c m\left ( t \right )+n_I\left ( t \right ) \right ] \cos^2\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right ) \cos\left ( 2 \pi f_ct \right )$$
$$\Rightarrow v_2\left ( t \right )=\left [ A_c m\left ( t \right )+n_I\left ( t \right ) \right ] \left ( \frac{1+ \cos\left ( 4 \pi f_ct \right )}{2} \right ) -n_Q\left ( t \right )\frac{ \sin\left ( 4 \pi f_ct \right )}{2}$$
当上述信号作为低通滤波器的输入时,我们将得到低通滤波器的输出:
$$d\left ( t \right )=\frac{\left [ A_c m\left ( t \right )+n_I\left ( t \right ) \right ]}{2}$$
解调信号的平均功率为
$$P_m=\left ( \frac{A_cm\left ( t \right )}{2\sqrt{2}} \right )^2=\frac{{A_{c}}^{2}P}{8 }$$
输出端噪声的平均功率为
$$P_{否}=\frac{WN_0}{4}$$
将这些值代入输出 SNR公式中。
$$\left ( SNR \right )_{O,DSBSC}= \frac {\:\: 解调信号 \:\: 的平均 \:\: 功率 \:\: {平均 \:\: 功率 \: \: 的 \:\: 噪音 \:\: 在 \:\: 输出}$$
$$\Rightarrow \left ( SNR \right )_{O,DSBSC}=\left ( \frac{{A_{c}}^{2}P}{8} \right )/ \left ( \frac{WN_0 }{4} \right )=\frac{{A_{c}}^{2}P}{2WN_0}$$
代入DSBSC 接收器公式的品质因数中的值。
$$F=\frac{\left ( SNR \right )_{O,DSBSC}}{\left ( SNR \right )_{C,DSBSC}}$$
$$\Rightarrow F= \left ( \frac{{A_{c}}^{2}P}{2WN_0} \right )/ \left ( \frac{{A_{c}}^{2}P}{ 2WN_0} \右)$$
$$\右箭头 F= 1$$
因此,DSBSC 接收器的品质因数为 1。
SSBSC 系统中的 SNR 计算
考虑以下 SSBSC 系统的接收器模型来分析噪声。
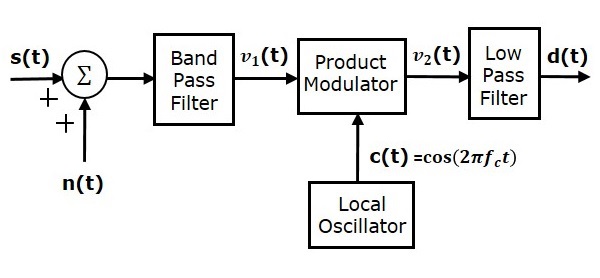
我们知道具有下边带的 SSBSC 调制波为
$$s\left ( t \right )=\frac{A_mA_c}{2} \cos \left [ 2 \pi\left ( f_c-f_m \right )t \right ]$$
SSBSC调制波的平均功率为
$$P_s=\left ( \frac{A_mA_c}{2\sqrt{2}} \right )^2=\frac{{A_{m}}^{2}{A_{c}}^{2}} {8}$$
消息带宽中的平均噪声功率为
$$P_{nc}=WN_0$$
将这些值代入信道 SNR 公式中。
$$\left ( SNR \right )_{C,SSBSC}= \frac {\:\: SSBSC \:\: 调制波的平均 \:\: 功率 \:\: {平均 \: \:\: 消息\:\: 中的\:\: 噪声\:\: 功率\:\: 带宽}$$
$$\Rightarrow \left (信噪比\right)_{C,SSBSC}=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8WN_0}$$
假设带通噪声与SSBSC调制波在通道中混合,如上图所示。该组合用作乘积调制器的输入之一。因此,该乘积调制器的输入是
$$v_1\left ( t \right )=s\left ( t \right )+n\left ( t \right )$$
$$v_1\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c-f_m \right )t \right ] + n_I\left ( t \right ) \ cos\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin \left ( 2 \pi f_ct \right )$$
本地振荡器产生载波信号$c\left ( t \right )= \cos \left ( 2 \pi f_ct \right ) $。该信号用作乘积调制器的另一个输入。因此,乘积调制器产生一个输出,它是 $v_1\left ( t \right )$ 和 $c\left ( t \right )$ 的乘积。
$$v_2\left ( t \right )=v_1\left ( t \right )c \left ( t \right )$$
将 $v_1\left ( t \right )$ 和 $ c\left ( t \right )$ 值代入上述方程中。
$\Rightarrow v_2(t)= (\frac{A_mA_c}{2} \cos[ 2 \pi ( f_c-f_m )t ] + n_I ( t ) \cos ( 2 \pi f_ct )-$
$n_Q( t ) \sin ( 2 \pi f_ct ) )\cos ( 2 \pi f_ct )$
$\Rightarrow v_2\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c-f_m \right )t \right ] \cos\left ( 2 \pi f_ct \右)+$
$n_I\left ( t \right ) \cos^2\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right ) \cos\left ( 2 \pi f_ct \右)$
$\Rightarrow v_2\left ( t \right )=\frac{A_mA_c}{4} \left \{ \cos\left [ 2 \pi\left ( 2f_c-f_m \right )t \right ] + \cos \left ( 2 \pi f_mt \right )\right \}+$
$n_I\left ( t \right )\left ( \frac{1+ \cos\left ( 4 \pi f_ct \right )}{2} \right )- n_Q\left ( t \right )\frac{\sin \left ( 4 \pi f_ct \right )}{2}$
当上述信号作为低通滤波器的输入时,我们将得到低通滤波器的输出:
$$d\left ( t \right )=\frac{A_mA_c}{2} \cos\left ( 2 \pi f_mt \right )+\frac{n_I\left ( t \right )}{2}$$
解调信号的平均功率为
$$P_m=\left ( \frac{A_mA_c}{4\sqrt{2}} \right )^2=\frac{{A_{m}}^{2}{A_{c}}^{2}} {32}$$
输出端噪声的平均功率为
$$P_{否}=\frac{WN_0}{4}$$
将这些值代入输出SNR公式中
$$\left ( SNR \right )_{O,SSBSC}= \frac {\:\: 解调信号 \:\: 的平均 \:\: 功率 \:\:}{平均 \:\: 功率 \: \: 的\:\: 噪音\:\: 在\:\: 输出}$$
$$\Rightarrow \left ( SNR \right )_{O,SSBSC}= \left ( \frac{{A_{m}}^{2}{A_{c}}^{2}}{32} \right )/\left ( \frac{WN_0}{4} \right )=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8WN_0}$$
代入SSBSC接收器公式的品质因数中的值
$$F=\frac{\left ( SNR \right )_{O,SSBSC}}{\left ( SNR \right )_{C,SSBSC}}$$
$$F=\left ( \frac{{A_{m}}^{2}{A_{c}}^{2}}{8WN_0} \right )/\left ( \frac{{A_{m}} ^{2}{A_{c}}^{2}}{8WN_0} \右)$$
$$F=1$$
因此,SSSBC 接收器的品质因数为 1。
