宇宙学 - 凌日法
使用凌日法(开普勒太空望远镜)来确定其大小。行星引起的恒星亮度下降通常与双星系统不太相似。
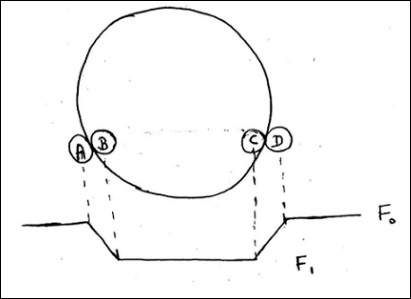
F 0是行星遮挡恒星之前恒星的通量。
F 1是整个行星在恒星前面后的通量。
下图将用于所有计算。
$$\frac{F_0 - F_1}{F_0} = \frac{\pi r_p^{2}}{\pi R^2_\ast}$$
$$\frac{\Delta F}{F} \cong \frac{r^2_p}{R^2_\ast}$$
$$\left (\frac{\Delta F}{F} \right )_{earth} \cong 0.001\%$$
$$\left ( \frac{\Delta F}{F} \right )_{jupiter} \cong 1\%$$
这对于地面望远镜来说并不容易实现。这是通过哈勃望远镜实现的。
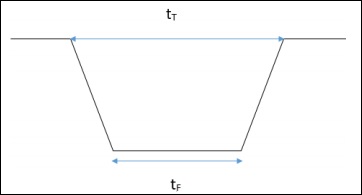
这里,$t_T$是位置A和D之间的时间,$t_F$是位置B和C之间的时间。
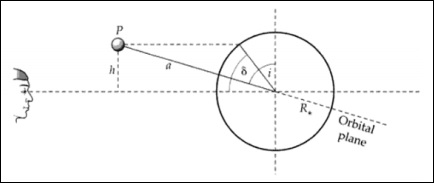
凌日的几何形状与系统的倾角i相关。凌日纬度和倾角是可以互换的。
从上面的图像中,我们可以写出 -
$$\frac{h}{a} = cos(i)$$
$$\frac{h}{R_\ast} = sin(\delta)$$
$$cos(i) = \frac{R_\ast sin(\delta)}{a}$$
$$y^2 = (R_\ast + R_p)^2 - h^2$$
$$y = [(R_\ast + R_p)^2 - h^2]^{\frac{1}{2}}$$
$$sin(\theta) = \frac{y}{a}$$
$$\theta = sin^{-1}\left [ \frac{(R_\ast + R_p)^2 - a^2cos^2(i)}{a^2} \right ]^{\frac{1 }{2}}$$
$$t_T = \frac{P}{2\pi} \times 2\theta$$
这里,$t_T$ 是凌日发生的时间段的分数,(2θ/2π) 是凌日发生的角度的分数。
$$sin(\frac{t_T\pi}{P}) = \frac{R_\ast}{a}\left [ \left ( 1+ \frac{R_p}{R_\ast}\right )^2 - \left ( \frac{a}{R_\ast}cos(i)\right )^2 \right ]^{\frac{1}{2}}$$
通常,a>>R*>>Rp。所以,我们可以写 -
$$sin(\frac{t_T\pi}{P}) = \frac{R_\ast}{a}\left [ 1- \left ( \frac{a}{R_\ast}cos(i) \right )^2\右]^{\frac{1}{2}}$$
这里,P是两次连续传输之间的持续时间。与轨道时间周期相比,传输时间要短得多。因此,
$$t_T = \frac{P}{\pi}\left [ \left ( \frac{R_\ast}{a}\right )^2 - cos^2(i)\right ]^{\frac{1 }{2}}$$
这里,t T、P、R*是可观测量,a和i应该被找出。
现在,
$$sin(\frac{t_F\pi}{P}) = \frac{R_\ast}{a}\left [\left (1 - \frac{R_p}{R_\ast} \right )^2 - \left ( \frac{a}{R_\ast}cos\:i \right )^2\right ]^{\frac{1}{2}}$$
其中,$y^2 = (R_\ast − R_p)^2 − h^2$。
让,
$$\frac{\Delta F}{F} = D = \left ( \frac{R_p}{R_\ast} \right )^2$$
现在,我们可以表达,
$$\frac{a}{R_\ast} = \frac{2P}{\pi} D^{\frac{1}{4}}(t^2_T - t^2_F)^{-\frac{1 }{2}}$$
对于主序星来说,
$$R_\ast \propto M^\alpha_\ast$$
$$\frac{R_\ast}{R_0} \propto \left ( \frac{M_\ast}{M_0}\right )^\alpha$$
这给出了R*。
因此,我们也得到了“a”的值。
因此,我们得到“R p ”、“ap”,甚至“i”。
对于这一切,
$$h \leq R_\ast + R_p$$
$$a\: cos\: i \leq R_\ast + R_p$$
对于甚至
