
- 控制系统教程
- 控制系统 - 主页
- 控制系统 - 简介
- 控制系统 - 反馈
- 数学模型
- 机械系统建模
- 机械系统的电气类比
- 控制系统 - 框图
- 框图代数
- 框图简化
- 信号流图
- 梅森增益公式
- 时间响应分析
- 一阶系统的响应
- 二阶系统响应
- 时域规格
- 稳态误差
- 控制系统 - 稳定性
- 控制系统 - 稳定性分析
- 控制系统 - 根轨迹
- 根轨迹的构建
- 频率响应分析
- 控制系统 - 波特图
- 波特图的构建
- 控制系统 - 极坐标图
- 控制系统 - 奈奎斯特图
- 控制系统 - 补偿器
- 控制系统 - 控制器
- 控制系统 - 状态空间模型
- 状态空间分析
- 控制系统有用的资源
- 控制系统 - 快速指南
- 控制系统 - 有用资源
- 控制系统 - 讨论
控制系统 - 快速指南
控制系统 - 简介
控制系统是通过控制输出来提供所需响应的系统。下图显示了控制系统的简单框图。

这里,控制系统由单个块表示。由于输出是通过变化的输入来控制的,因此控制系统因此得名。我们将通过某种机制改变这个输入。在关于开环和闭环控制系统的下一节中,我们将详细研究控制系统内部的块以及如何改变此输入以获得所需的响应。
示例- 交通灯控制系统、洗衣机
交通灯控制系统是控制系统的一个例子。这里,一系列输入信号被施加到该控制系统,并且输出是将在一段时间内亮起的三个灯之一。在此期间,另外两个灯将熄灭。根据特定路口的交通研究,可以确定灯的打开和关闭时间。因此,输入信号控制输出。因此,交通灯控制系统是按时间运行的。
控制系统的分类
根据一些参数,我们可以将控制系统分为以下几种。
连续时间和离散时间控制系统
根据所使用信号的类型,控制系统可以分为连续时间控制系统和离散时间控制系统。
在连续时间控制系统中,所有信号在时间上都是连续的。但是,在离散时间控制系统中,存在一个或多个离散时间信号。
SISO 和 MIMO 控制系统
根据输入和输出的数量,控制系统可分为 SISO 控制系统和 MIMO 控制系统。
SISO(单输入和单输出)控制系统有一个输入和一个输出。而MIMO(多输入多输出)控制系统具有多个输入和多个输出。
开环和闭环控制系统
控制系统根据反馈路径可分为开环控制系统和闭环控制系统。
在开环控制系统中,输出不会反馈到输入。因此,控制动作独立于所需的输出。
下图显示了开环控制系统的框图。

这里,输入被施加到控制器并产生驱动信号或控制信号。该信号作为要控制的工厂或过程的输入给出。因此,工厂产生的输出是受控的。我们之前讨论的交通灯控制系统是开环控制系统的一个例子。
在闭环控制系统中,输出反馈到输入。因此,控制动作取决于所需的输出。
下图为负反馈闭环控制系统框图。

误差检测器产生误差信号,该信号是输入信号和反馈信号之间的差值。通过将整个系统的输出视为该块的输入,从该块(反馈元件)获得该反馈信号。误差信号不是直接输入,而是作为控制器的输入。
因此,控制器产生控制设备的驱动信号。在这种组合中,控制系统的输出会自动调整,直到获得所需的响应。因此,闭环控制系统也称为自动控制系统。输入端具有传感器的交通灯控制系统是闭环控制系统的一个示例。
开环和闭环控制系统之间的差异如下表所示。
| 开环控制系统 | 闭环控制系统 |
|---|---|
| 控制动作独立于所需的输出。 | 控制动作取决于所需的输出。 |
| 反馈路径不存在。 | 存在反馈路径。 |
| 这些也称为非反馈控制系统。 | 这些也称为反馈控制系统。 |
| 易于设计。 | 设计困难。 |
| 这些都是经济的。 | 这些都比较贵。 |
| 不准确。 | 准确的。 |
控制系统 - 反馈
如果输出或输出的某些部分返回到输入侧并用作系统输入的一部分,则称为反馈。反馈对于提高控制系统的性能起着重要作用。在本章中,让我们讨论反馈的类型和反馈的效果。
反馈类型
有两种类型的反馈 -
- 正面反馈
- 负面反馈
正面反馈
正反馈将参考输入、$R(s)$ 和反馈输出相加。下图为正反馈控制系统框图。

传递函数的概念将在后面的章节中讨论。暂且考虑正反馈控制系统的传递函数为,
$T=\frac{G}{1-GH}$ (方程 1)
在哪里,
T是正反馈控制系统的传递函数或总增益。
G是开环增益,是频率的函数。
H是反馈路径的增益,是频率的函数。
负面反馈
负反馈减少了参考输入、$R(s)$ 和系统输出之间的误差。下图所示为负反馈控制系统的框图。

负反馈控制系统的传递函数为,
$T=\frac{G}{1+GH}$ (方程 2)
在哪里,
T是负反馈控制系统的传递函数或总增益。
G是开环增益,是频率的函数。
H是反馈路径的增益,是频率的函数。
上述传递函数的推导将在后面的章节中介绍。
反馈的影响
现在让我们了解反馈的影响。
反馈对总体增益的影响
从公式2可以看出,负反馈闭环控制系统的总增益是“G”与(1+GH)的比值。因此,总增益可能会根据 (1+GH) 的值而增加或减少。
如果(1+GH)的值小于1,则总体增益增加。在这种情况下,“GH”值为负,因为反馈路径的增益为负。
如果(1+GH)的值大于1,则总体增益减小。在这种情况下,“GH”值为正,因为反馈路径的增益为正。
一般来说,“G”和“H”是频率的函数。因此,反馈将在一个频率范围内增加系统的整体增益,并在另一频率范围内减少系统的整体增益。
反馈对灵敏度的影响
负反馈闭环控制系统总增益 ( T ) 对开环增益 ( G )变化的敏感度定义为
$S_{G}^{T} = \frac{\frac{\partial T}{T}}{\frac{\partial G}{G}}=\frac{百分比\: 变化 \: 在 \:T 中{百分比\: 改变\: in \:G}$ (公式 3)
其中,∂T是由于 G 的增量变化而引起的 T 的增量变化。
我们可以将方程 3 重写为
$S_{G}^{T}=\frac{\partial T}{\partial G}\frac{G}{T}$ (方程 4)
对方程 2 两边的 G 进行偏微分。
$\frac{\partial T}{\partial G}=\frac{\partial}{\partial G}\left (\frac{G}{1+GH} \right )=\frac{(1+GH) .1-G(H)}{(1+GH)^2}=\frac{1}{(1+GH)^2}$ (等式5)
从方程 2 中,您将得到
$\frac{G}{T}=1+GH$ (方程 6)
将公式 5 和公式 6 代入公式 4。
$$S_{G}^{T}=\frac{1}{(1+GH)^2}(1+GH)=\frac{1}{1+GH}$$
这样,我们就得到了闭环控制系统总增益的灵敏度为(1+GH)的倒数。因此,灵敏度可能会根据 (1+GH) 的值而增加或减少。
如果(1+GH)的值小于1,则灵敏度增加。在这种情况下,“GH”值为负,因为反馈路径的增益为负。
如果(1+GH)的值大于1,则灵敏度降低。在这种情况下,“GH”值为正,因为反馈路径的增益为正。
一般来说,“G”和“H”是频率的函数。因此,反馈将提高系统增益在一个频率范围内的灵敏度,而在另一频率范围内降低系统增益的灵敏度。因此,我们必须以系统对参数变化不敏感或不太敏感的方式选择“GH”值。
反馈对稳定性的影响
如果系统的输出受到控制,则称该系统是稳定的。否则,就说它不稳定。
在方程2中,如果分母值为零(即GH = -1),则控制系统的输出将为无穷大。因此,控制系统变得不稳定。
因此,必须正确选择反馈量,才能使控制系统稳定。
反馈对噪声的影响
为了了解反馈对噪声的影响,让我们比较仅由噪声信号引起的有反馈和无反馈的传递函数关系。
考虑一个带有噪声信号的开环控制系统,如下所示。

仅由噪声信号引起的开环传递函数为
$\frac{C(s)}{N(s)}=G_b$ (方程 7)
它是通过使另一个输入 $R(s)$ 等于 0 来获得的。
考虑一个带有噪声信号的闭环控制系统,如下所示。

仅由噪声信号引起的闭环传递函数为
$\frac{C(s)}{N(s)}=\frac{G_b}{1+G_aG_bH}$ (方程8)
它是通过使另一个输入 $R(s)$ 等于 0 来获得的。
比较公式 7 和公式 8,
在闭环控制系统中,只要 $(1+G_a G_b H)$ 项大于 1,噪声信号引起的增益就会减少 $(1+G_a G_b H)$ 倍。
控制系统 - 数学模型
控制系统可以用一组称为数学模型的数学方程来表示。这些模型对于控制系统的分析和设计很有用。控制系统分析就是在已知输入和数学模型的情况下求出输出。控制系统的设计就是在已知输入和输出的情况下找到数学模型。
主要使用以下数学模型。
- 微分方程模型
- 传递函数模型
- 状态空间模型
让我们讨论本章的前两个模型。
微分方程模型
微分方程模型是控制系统的时域数学模型。对于微分方程模型,请遵循以下步骤。
将基本定律应用于给定的控制系统。
通过消除中间变量,得到输入和输出的微分方程。
例子
考虑如下图所示的电气系统。该电路由电阻器、电感器和电容器组成。所有这些电气元件都是串联的。施加到该电路的输入电压是$v_i$,电容器两端的电压是输出电压$v_o$。

该电路的网格方程为
$$v_i=Ri+L\frac{\text{d}i}{\text{d}t}+v_o$$
代入上式中通过电容器的电流$i=c\frac{\text{d}v_o}{\text{d}t}$。
$$\Rightarrow\:v_i=RC\frac{\text{d}v_o}{\text{d}t}+LC\frac{\text{d}^2v_o}{\text{d}t^2} +v_o$$
$$\Rightarrow\frac{\text{d}^2v_o}{\text{d}t^2}+\left ( \frac{R}{L} \right )\frac{\text{d}v_o} {\text{d}t}+\left ( \frac{1}{LC} \right )v_o=\left ( \frac{1}{LC} \right )v_i$$
上式是二阶微分方程。
传递函数模型
传递函数模型是控制系统的s域数学模型。线性时不变(LTI)系统的传递函数被定义为假设所有初始条件为零,输出的拉普拉斯变换与输入的拉普拉斯变换的比率。
如果$x(t)$和$y(t)$是LTI系统的输入和输出,则相应的拉普拉斯变换是$X(s)$和$Y(s)$。
因此,LTI系统的传递函数等于$Y(s)$与$X(s)$之比。
$$即,\: 转移\: 函数 =\frac{Y(s)}{X(s)}$$
LTI系统的传递函数模型如下图所示。

在这里,我们表示一个 LTI 系统,其中包含一个内部具有传递函数的块。该块有一个输入 $X(s)$ 和输出 $Y(s)$。
例子
之前,我们得到了电力系统的微分方程为
$$\frac{\text{d}^2v_o}{\text{d}t^2}+\left ( \frac{R}{L} \right )\frac{\text{d}v_o}{\文本{d}t}+\left (\frac{1}{LC} \right)v_o=\left (\frac{1}{LC} \right)v_i$$
在两侧应用拉普拉斯变换。
$$s^2V_o(s)+\left ( \frac{sR}{L} \right )V_o(s)+\left ( \frac{1}{LC} \right )V_o(s)=\left ( \frac{1}{LC} \right )V_i(s)$$
$$\Rightarrow \left \{ s^2+\left ( \frac{R}{L} \right )s+\frac{1}{LC} \right \}V_o(s)=\left ( \frac{ 1}{LC} \右 )V_i(s)$$
$$\Rightarrow \frac{V_o(s)}{V_i(s)}=\frac{\frac{1}{LC}}{s^2+\left ( \frac{R}{L} \right ) s+\frac{1}{LC}}$$
在哪里,
$v_i(s)$ 是输入电压 $v_i$ 的拉普拉斯变换
$v_o(s)$ 是输出电压 $v_o$ 的拉普拉斯变换
上式是二阶电力系统的传递函数。该系统的传递函数模型如下所示。

在这里,我们展示了一个二阶电气系统,其中包含一个内部具有传递函数的块。该块有一个输入 $V_i(s)$ 和一个输出 $V_o(s)$。
机械系统建模
在本章中,我们将讨论机械系统的微分方程建模。根据运动类型,有两种类型的机械系统。
- 平移机械系统
- 旋转机械系统
平移机械系统的建模
平移机械系统沿直线移动。这些系统主要由三个基本要素组成。这些是质量、弹簧和缓冲器或阻尼器。
如果向平移机械系统施加力,则由于系统的质量、弹性和摩擦力,该力会受到相反的力的抵抗。由于施加的力和相反的力方向相反,因此作用在系统上的力的代数和为零。现在让我们分别看看这三个元素所反对的力量。
大量的
质量是物体的属性,它储存动能。如果对质量为M 的物体施加力,则由于质量而会受到相反的力的抵抗。该反作用力与身体的加速度成正比。假设弹性和摩擦力可以忽略不计。
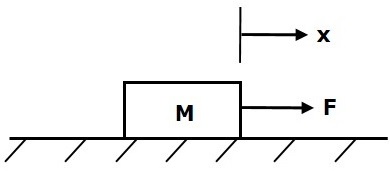
$$F_m\propto\: a$$
$$\Rightarrow F_m=Ma=M\frac{\text{d}^2x}{\text{d}t^2}$$
$$F=F_m=M\frac{\text{d}^2x}{\text{d}t^2}$$
在哪里,
F是施加的力
F m是质量产生的反作用力
M是质量
a是加速度
x是位移
春天
春天是一种元素,储存着势能。如果对弹簧K施加力,则由于弹簧的弹性,该力会受到相反的力的抵抗。该反作用力与弹簧的位移成正比。假设质量和摩擦力可以忽略不计。
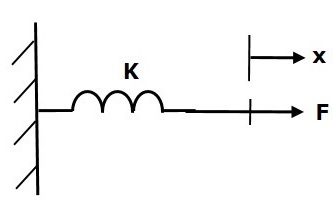
$$F\propto\: x$$
$$\右箭头 F_k=Kx$$
$$F=F_k=Kx$$
在哪里,
F是施加的力
F k是弹簧弹性产生的反作用力
K是弹簧常数
x是位移
缓冲器
如果在缓冲器B上施加力,则由于缓冲器的摩擦力,该力会受到相反的力的抵抗。该反作用力与物体的速度成正比。假设质量和弹性可以忽略不计。

$$F_b\propto\: \nu$$
$$\Rightarrow F_b=B\nu=B\frac{\text{d}x}{\text{d}t}$$
$$F=F_b=B\frac{\text{d}x}{\text{d}t}$$
在哪里,
F b是阻尼器摩擦产生的反作用力
B为摩擦系数
v是速度
x是位移
旋转机械系统建模
旋转机械系统绕固定轴移动。这些系统主要由三个基本要素组成。它们是转动惯量、扭转弹簧和缓冲器。
如果将扭矩施加到旋转机械系统,则由于系统的惯性矩、弹性和摩擦力,扭矩会受到反向扭矩的抵抗。由于施加的扭矩和相反的扭矩方向相反,所以作用在系统上的扭矩的代数和为零。现在让我们分别看看这三个元件所反对的扭矩。
转动惯量
在平动机械系统中,质量存储动能。类似地,在旋转机械系统中,转动惯量存储动能。
如果将扭矩施加到具有转动惯量J的物体上,则由于转动惯量,该扭矩会受到相反扭矩的抵抗。该反向扭矩与主体的角加速度成正比。假设弹性和摩擦力可以忽略不计。

$$T_j\propto\: \alpha$$
$$\Rightarrow T_j=J\alpha=J\frac{\text{d}^2\theta}{\text{d}t^2}$$
$$T=T_j=J\frac{\text{d}^2\theta}{\text{d}t^2}$$
在哪里,
T是施加的扭矩
T j是由于惯性矩而产生的反向扭矩
J是转动惯量
α是角加速度
θ是角位移
扭转弹簧
在平动机械系统中,弹簧储存势能。类似地,在旋转机械系统中,扭转弹簧存储势能。
如果在扭转弹簧K上施加扭矩,则由于扭转弹簧的弹性,该扭矩会受到反向扭矩的抵抗。该反向扭矩与扭转弹簧的角位移成正比。假设惯性矩和摩擦力可以忽略不计。

$$T_k\propto\: \theta$$
$$\右箭头 T_k=K\theta$$
$$T=T_k=K\theta$$
在哪里,
T是施加的扭矩
T k是扭簧弹性产生的反向扭矩
K是扭转弹簧常数
θ是角位移
缓冲器
如果在缓冲器B上施加扭矩,则会由于缓冲器的旋转摩擦而受到反向扭矩的抵抗。该反向扭矩与物体的角速度成正比。假设惯性矩和弹性矩可以忽略不计。

$$T_b\propto\: \omega$$
$$\Rightarrow T_b=B\omega=B\frac{\text{d}\theta}{\text{d}t}$$
$$T=T_b=B\frac{\text{d}\theta}{\text{d}t}$$
在哪里,
T b是阻尼器旋转摩擦产生的反向扭矩
B是旋转摩擦系数
ω是角速度
θ是角位移
机械系统的电气类比
如果满足以下两个条件,则称两个系统彼此相似。
- 这两个系统在物理上是不同的
- 这两个系统的微分方程建模相同
电气系统和机械系统是两个物理上不同的系统。平移机械系统有两种类型的电气类比。这些是力电压类比和力电流类比。
力电压类比
在力电压类比中,将平移机械系统的数学方程与电气系统的网格方程进行比较。
考虑如下平移机械系统,如下图所示。

该系统的力平衡方程为
$$F=F_m+F_b+F_k$$
$\Rightarrow F=M\frac{\text{d}^2x}{\text{d}t^2}+B\frac{\text{d}x}{\text{d}t}+Kx$ (公式 1)
考虑如下图所示的电气系统。该电路由电阻器、电感器和电容器组成。所有这些电气元件都是串联连接的。施加到该电路的输入电压为 $V$ 伏,流过该电路的电流为 $i$ 安培。

该电路的网格方程为
$V=Ri+L\frac{\text{d}i}{\text{d}t}+\frac{1}{c}\int idt$ (方程 2 )
将 $i=\frac{\text{d}q}{\text{d}t}$ 代入方程 2 中。
$$V=R\frac{\text{d}q}{\text{d}t}+L\frac{\text{d}^2q}{\text{d}t^2}+\frac{ q}{C}$$
$\Rightarrow V=L\frac{\text{d}^2q}{\text{d}t^2}+R\frac{\text{d}q}{\text{d}t}+\left ( \frac{1}{c} \right )q$ (方程 3)
通过比较式1和式3,我们可以得到平移机械系统和电气系统的类似量。下表显示了这些类似的数量。
| 平移机械系统 | 电子系统 |
|---|---|
| 力(F) | 电压(V) |
| 质量(M) | 电感(L) |
| 摩擦系数(B) | 电阻(R) |
| 弹簧常数(K) | 电容的倒数 $(\frac{1}{c})$ |
| 位移(x) | 电荷(q) |
| 速度(v) | 电流(i) |
类似地,旋转机械系统也有扭矩电压类比。现在让我们讨论一下这个类比。
扭矩电压类比
在这个类比中,旋转机械系统的数学方程与电气系统的网格方程进行了比较。
旋转机械系统如下图所示。

扭矩平衡方程为
$$T=T_j+T_b+T_k$$
$\Rightarrow T=J\frac{\text{d}^2\theta}{\text{d}t^2}+B\frac{\text{d}\theta}{\text{d}t} +k\theta$ (方程 4)
通过比较式4和式3,我们可以得到旋转机械系统和电气系统的类似量。下表显示了这些类似的数量。
| 旋转机械系统 | 电子系统 |
|---|---|
| 扭矩(T) | 电压(V) |
| 转动惯量(J) | 电感(L) |
| 旋转摩擦系数(B) | 电阻(R) |
| 扭转弹簧常数(K) | 电容的倒数 $(\frac{1}{c})$ |
| 角位移(θ) | 电荷(q) |
| 角速度(ω) | 电流(i) |
力电流类比
在力电流类比中,将平移机械系统的数学方程与电气系统的节点方程进行比较。
考虑如下图所示的电气系统。该电路由电流源、电阻、电感和电容组成。所有这些电气元件都是并联连接的。

节点方程为
$i=\frac{V}{R}+\frac{1}{L}\int Vdt+C\frac{\text{d}V}{\text{d}t}$(方程 5 )
将 $V=\frac{\text{d}\Psi}{\text{d}t}$ 代入方程 5。
$$i=\frac{1}{R}\frac{\text{d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi+C \frac{\text{d}^2\Psi}{\text{d}t^2}$$
$\Rightarrow i=C\frac{\text{d}^2\Psi}{\text{d}t^2}+\left ( \frac{1}{R} \right )\frac{\text{ d}\Psi}{\text{d}t}+\left ( \frac{1}{L} \right )\Psi$ (方程 6)
通过比较式1和式6,我们可以得到平移机械系统和电气系统的类似量。下表显示了这些类似的数量。
| 平移机械系统 | 电子系统 |
|---|---|
| 力(F) | 电流(i) |
| 质量(M) | 电容(C) |
| 摩擦系数(B) | 阻力的倒数$(\frac{1}{R})$ |
| 弹簧常数(K) | 电感的倒数$(\frac{1}{L})$ |
| 位移(x) | 磁通量(ψ) |
| 速度(v) | 电压(V) |
类似地,旋转机械系统有一个扭矩电流类比。现在让我们讨论这个类比。
扭矩电流类比
在这个类比中,将旋转机械系统的数学方程与电气系统的节点网格方程进行比较。
通过比较式4和式6,我们可以得到旋转机械系统和电气系统的类似量。下表显示了这些类似的数量。
| 旋转机械系统 | 电子系统 |
|---|---|
| 扭矩(T) | 电流(i) |
| 转动惯量(J) | 电容(C) |
| 旋转摩擦系数(B) | 阻力的倒数$(\frac{1}{R})$ |
| 扭转弹簧常数(K) | 电感的倒数$(\frac{1}{L})$ |
| 角位移(θ) | 磁通量(ψ) |
| 角速度(ω) | 电压(V) |
在本章中,我们讨论了机械系统的电气类比。这些类比有助于从类比电气系统中研究和分析机械系统等非电气系统。
控制系统 - 框图
框图由单个块或块的组合组成。这些用于以图形形式表示控制系统。
框图的基本元素
框图的基本元素是块、求和点和出发点。让我们考虑下图所示的闭环控制系统框图来识别这些元件。

上面的框图由两个具有传递函数 G(s) 和 H(s) 的块组成。它还具有一个总结点和一个起飞点。箭头表示信号流的方向。现在让我们一一讨论这些要素。
堵塞
组件的传递函数由块表示。模块具有单输入和单输出。
下图显示了具有输入 X(s)、输出 Y(s) 和传递函数 G(s) 的块。

传递函数,$G(s)=\frac{Y(s)}{X(s)}$
$$\右箭头 Y(s)=G(s)X(s)$$
通过将块的传递函数与输入相乘来获得块的输出。
求和点
求和点用内部带有十字 (X) 的圆圈表示。它有两个或多个输入和单个输出。它产生输入的代数和。它还根据输入的极性执行输入的求和或减法或求和与减法的组合。让我们一一看看这三个操作。
下图显示了具有两个输入(A、B)和一个输出(Y)的求和点。这里,输入 A 和 B 具有正号。因此,求和点产生输出 Y,即A 和 B 之和。
即,Y = A + B。

下图显示了具有两个输入(A、B)和一个输出(Y)的求和点。这里,输入A和B具有相反的符号,即,A具有正号而B具有负号。因此,求和点产生输出Y作为A 和 B 的差。
Y = A + (-B) = A - B。

下图显示了具有 3 个输入(A、B、C)和 1 个输出(Y)的求和点。这里,输入 A 和 B 具有正号,而 C 具有负号。因此,求和点产生的输出Y为
Y = A + B + (−C) = A + B − C。

起飞点
出发点是同一输入信号可以通过多个分支的点。这意味着在起飞点的帮助下,我们可以将相同的输入应用于一个或多个块,求和点。
在下图中,出发点用于将相同的输入 R(s) 连接到另外两个块。
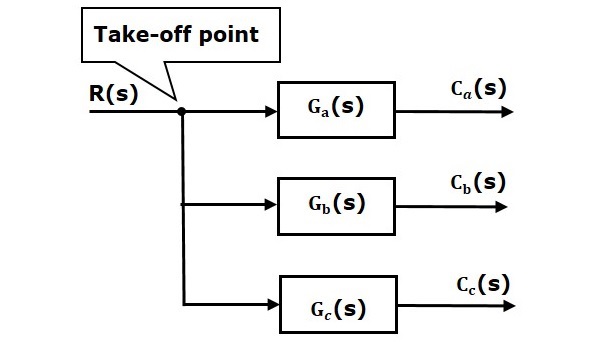
在下图中,出发点用于连接输出C(s),作为求和点的输入之一。

电气系统的框图表示
在本节中,让我们用框图来表示一个电气系统。电气系统主要包含三个基本元件——电阻器、电感器和电容器。
考虑一系列 RLC 电路,如下图所示。其中,V i (t)和V o (t)是输入和输出电压。令 i(t) 为通过电路的电流。该电路是时域电路。

通过对该电路应用拉普拉斯变换,将得到s域中的电路。电路如下图所示。

根据上面的电路,我们可以写出
$$I(s)=\frac{V_i(s)-V_o(s)}{R+sL}$$
$\Rightarrow I(s)=\left \{ \frac{1}{R+sL} \right \}\left \{ V_i(s)-V_o(s) \right \}$ (方程 1 )
$V_o(s)=\left ( \frac{1}{sC} \right )I(s)$ (方程 2)
现在让我们分别绘制这两个方程的框图。然后将这些框图适当组合,即可得到串联RLC电路(s域)的总体框图。
方程 1 可以通过具有传递函数 $\frac{1}{R+sL}$ 的模块来实现。该块的输入和输出为$\left \{ V_i(s)-V_o(s) \right \}$ 和$I(s)$。我们需要一个求和点来得到$\left \{ V_i(s)-V_o(s) \right \}$。公式 1 的框图如下图所示。

方程 2 可以使用具有传递函数 $\frac{1}{sC}$ 的模块来实现。该块的输入和输出是$I(s)$和$V_o(s)$。公式 2 的框图如下图所示。

该系列RLC电路(s域)的整体框图如下图所示。
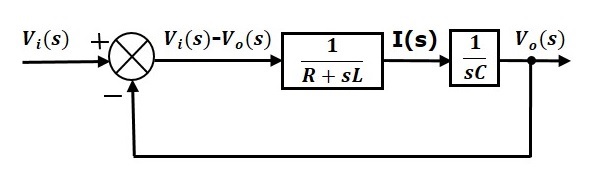
同样,您只需遵循这个简单的过程就可以绘制任何电路或系统的框图。
通过应用拉普拉斯变换将时域电路转换为 s 域电路。
写下流过所有串联支路元件的电流和所有并联支路上的电压的方程。
分别画出上述所有方程的框图。
将所有这些框图正确组合以获得电路(s 域)的总体框图。
控制系统 - 框图代数
框图代数只不过是涉及框图基本元素的代数。该代数涉及代数方程的图形表示。
块的基本连接
两个块之间存在三种基本连接类型。
串联
串联也称为级联。在下图中,两个具有传递函数 $G_1(s)$ 和 $G_2(s)$ 的块串联连接。

对于这种组合,我们将得到输出 $Y(s)$ 为
$$Y(s)=G_2(s)Z(s)$$
其中,$Z(s)=G_1(s)X(s)$
$$\右箭头 Y(s)=G_2(s)[G_1(s)X(s)]=G_1(s)G_2(s)X(s)$$
$$\Rightarrow Y(s)=\lbrace G_1(s)G_2(s)\rbrace X(s)$$
将此方程与输出方程的标准形式 $Y(s)=G(s)X(s)$ 进行比较。其中,$G(s) = G_1(s)G_2(s)$。
这意味着我们可以用一个块来表示两个块的串联连接。该单个块的传递函数是这两个块的传递函数的乘积。等效框图如下所示。

同样,您可以用单个块来表示“n”个块的串联连接。该单个块的传递函数是所有那些“n”个块的传递函数的乘积。
并联
并联连接的模块将具有相同的输入。在下图中,两个具有传递函数 $G_1(s)$ 和 $G_2(s)$ 的块并联连接。这两个块的输出连接到求和点。

对于这种组合,我们将得到输出 $Y(s)$ 为
$$Y(s)=Y_1(s)+Y_2(s)$$
其中,$Y_1(s)=G_1(s)X(s)$ 和 $Y_2(s)=G_2(s)X(s)$
$$\Rightarrow Y(s)=G_1(s)X(s)+G_2(s)X(s)=\lbrace G_1(s)+G_2(s)\rbrace X(s)$$
将此方程与输出方程的标准形式 $Y(s)=G(s)X(s)$ 进行比较。
其中,$G(s)=G_1(s)+G_2(s)$。
这意味着我们可以用一个块来表示两个块的并行连接。该单个块的传递函数是这两个块的传递函数之和。等效框图如下所示。

类似地,您可以用单个块来表示“n”个块的并行连接。该单个块的传递函数是所有那些“n”个块的传递函数的代数和。
反馈连接
正如我们在前面的章节中讨论的,反馈有两种类型——正反馈和负反馈。下图所示为负反馈控制系统。这里,具有传递函数 $G(s)$ 和 $H(s)$ 的两个块形成一个闭环。

求和点的输出为 -
$$E(s)=X(s)-H(s)Y(s)$$
输出 $Y(s)$ 是 -
$$Y(s)=E(s)G(s)$$
将 $E(s)$ 值代入上述方程中。
$$Y(s)=\left \{ X(s)-H(s)Y(s)\r大括号 G(s) \right\}$$
$$Y(s)\left \{ 1+G(s)H(s)\rbrace = X(s)G(s) \right\}$$
$$\Rightarrow \frac{Y(s)}{X(s)}=\frac{G(s)}{1+G(s)H(s)}$$
因此,负反馈闭环传递函数为$\frac{G(s)}{1+G(s)H(s)}$
这意味着我们可以用一个块来表示两个块的负反馈连接。该单个块的传递函数是负反馈的闭环传递函数。等效框图如下所示。

同样,您可以用一个块来表示两个块的正反馈连接。该单块的传递函数是正反馈的闭环传递函数,即$\frac{G(s)}{1-G(s)H(s)}$
求和点的框图代数
相对于块移动求和点有两种可能性 -
- 在块之后移动求和点
- 在块之前移动求和点
现在我们就针对上述两种情况一一看看需要做哪些安排。
在块之后移动求和点
考虑下图所示的框图。这里,求和点出现在块之前。

求和点有两个输入 $R(s)$ 和 $X(s)$。它的输出是$\left\{R(s)+X(s)\right\}$。
因此,块 $G(s)$ 的输入是 $\left \{R(s)+X(s)\right \}$ ,其输出是 –
$$Y(s)=G(s)\左\{R(s)+X(s)\右\}$$
$\Rightarrow Y(s)=G(s)R(s)+G(s)X(s)$ (方程 1)
现在,将求和点移到块之后。该框图如下图所示。

块 $G(s)$ 的输出是 $G(s)R(s)$。
求和点的输出为
$Y(s)=G(s)R(s)+X(s)$ (方程 2)
比较公式 1 和公式 2。
两个方程中的第一项 $'G(s) R(s)'$ 相同。但是,第二项有所不同。为了使第二项也相同,我们还需要一个块 $G(s)$。它具有输入 $X(s)$,并且该块的输出作为求和点的输入而不是 $X(s)$ 给出。该框图如下图所示。
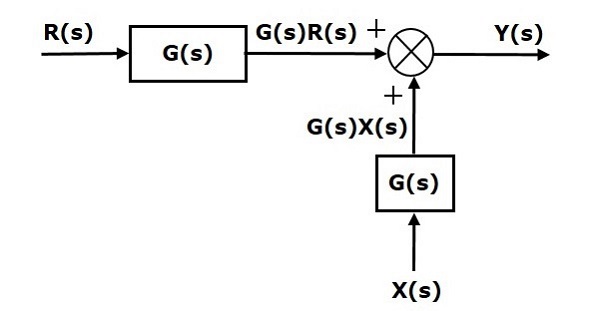
在块之前移动求和点
考虑下图所示的框图。这里,求和点出现在块之后。

该框图的输出是 -
$Y(s)=G(s)R(s)+X(s)$ (公式 3)
现在,将求和点移到块之前。该框图如下图所示。

该框图的输出是 -
$Y(S)=G(s)R(s)+G(s)X(s)$ (方程式 4)
比较公式 3 和公式 4,
第一项 $'G(s) R(s)'$ 在两个方程中相同。但是,第二项有所不同。为了使第二项也相同,我们还需要一个块 $\frac{1}{G(s)}$。它具有输入 $X(s)$,并且该块的输出作为求和点的输入而不是 $X(s)$ 给出。该框图如下图所示。

起飞点的框图代数
相对于块移动起飞点有两种可能性 -
- 在区块后移动起飞点
- 将起飞点移至区块之前
现在我们就针对上述两种情况,一一看看要作什么样的安排。
在区块后移动起飞点
考虑下图所示的框图。在这种情况下,起飞点位于块之前。

这里,$X(s)=R(s)$ 和 $Y(s)=G(s)R(s)$
当您将起飞点移到块之后时,输出 $Y(s)$ 将相同。但是,$X(s)$ 值存在差异。因此,为了获得相同的 $X(s)$ 值,我们需要多一个块 $\frac{1}{G(s)}$。它的输入为 $Y(s)$,输出为 $X(s)$。该框图如下图所示。

将起飞点移至区块之前
考虑下图所示的框图。在这里,起飞点位于块之后。

这里,$X(s)=Y(s)=G(s)R(s)$
当您将起飞点移动到块之前时,输出 $Y(s)$ 将相同。但是,$X(s)$ 值存在差异。因此,为了获得相同的 $X(s)$ 值,我们需要多一个块 $G(s)$。它的输入为 $R(s)$,输出为 $X(s)$。该框图如下图所示。

控制系统 - 框图简化
上一章讨论的概念有助于减少(简化)框图。
框图简化规则
请遵循以下规则来简化(简化)框图,该框图具有许多块、求和点和起飞点。
规则 1 - 检查串联连接的块并进行简化。
规则 2 - 检查并联连接的块并简化。
规则 3 - 检查反馈回路中连接的块并进行简化。
规则 4 - 如果简化时起飞点有困难,请将其向右移动。
规则 5 - 如果在简化时求和点有困难,请将其向左移动。
规则 6 - 重复上述步骤,直到得到简化形式,即单个块。
注- 该单个块中存在的传递函数是整个框图的传递函数。
例子
考虑下图所示的框图。让我们使用框图简化规则来简化(简化)该框图。

步骤 1 - 对块 $G_1$ 和 $G_2$ 使用规则 1。对块 $G_3$ 和 $G_4$ 使用规则 2。修改后的框图如下图所示。

步骤 2 - 对块 $G_1G_2$ 和 $H_1$ 使用规则 3。使用规则 4 将起飞点转移到块 $G_5$ 之后。修改后的框图如下图所示。

步骤 3 - 对块 $(G_3 + G_4)$ 和 $G_5$ 使用规则 1。修改后的框图如下图所示。

步骤 4 - 对块 $(G_3 + G_4)G_5$ 和 $H_3$ 使用规则 3。修改后的框图如下图所示。

步骤 5 - 对于串联连接的块使用规则 1。修改后的框图如下图所示。

步骤 6 - 对反馈回路中连接的块使用规则 3。修改后的框图如下图所示。这是简化的框图。

因此,系统的传递函数为
$$\frac{Y(s)}{R(s)}=\frac{G_1G_2G_5^2(G_3+G_4)}{(1+G_1G_2H_1)\lbrace 1+(G_3+G_4)G_5H_3\rbrace G_5-G_1G_2G_5 (G_3+G_4)H_2}$$
注- 请按照以下步骤计算具有多个输入的框图的传递函数。
步骤 1 - 通过一次考虑一个输入来查找框图的传递函数,并使其余输入为零。
步骤 2 - 对剩余输入重复步骤 1。
步骤 3 - 通过添加所有这些传递函数来获取总体传递函数。
对于复杂的系统,框图缩减过程需要更多时间。因为,我们必须在每个步骤之后绘制(部分简化的)框图。因此,为了克服这个缺点,请使用信号流图(表示)。
在接下来的两章中,我们将讨论与信号流图相关的概念,即如何从给定的框图表示信号流图,以及如何仅使用增益公式而不进行任何约简处理来计算传递函数。
控制系统 - 信号流图
信号流图是代数方程的图形表示。在本章中,我们将讨论与信号流图相关的基本概念,并学习如何绘制信号流图。
信号流图的基本元素
节点和分支是信号流图的基本元素。
节点
节点是代表变量或信号的点。节点分为三种类型:输入节点、输出节点和混合节点。
输入节点- 它是一个节点,仅具有传出分支。
输出节点- 它是一个节点,仅具有传入分支。
混合节点- 它是一个节点,同时具有传入和传出分支。
例子
让我们考虑以下信号流图来识别这些节点。

该信号流图中出现的节点是y 1 、 y 2、y 3和y 4。
y 1和y 4分别是输入节点和输出节点。
y 2和y 3是混合节点。
分支
分支是连接两个节点的线段。它既有增益又有方向。例如,上面的信号流图中有四个分支。这些分支的增益为a、b、c和-d。
信号流图的构建
让我们通过考虑以下代数方程来构建信号流图 -
$$y_2=a_{12}y_1+a_{42}y_4$$
$$y_3=a_{23}y_2+a_{53}y_5$$
$$y_4=a_{34}y_3$$
$$y_5=a_{45}y_4+a_{35}y_3$$
$$y_6=a_{56}y_5$$
该信号流图中将有六个节点(y 1、y 2、y 3、y 4、y 5和y 6)和八个分支。支路的增益为a 12、a 23、a 34、a 45、a 56、a 42、a 53和a 35。
要获得总体信号流图,请绘制每个方程的信号流图,然后组合所有这些信号流图,然后按照下面给出的步骤进行操作 -
步骤 1 - $y_2 = a_{13}y_1 + a_{42}y_4$ 的信号流图如下图所示。

步骤 2 - $y_3 = a_{23}y_2 + a_{53}y_5$ 的信号流图如下图所示。

步骤 3 - $y_4 = a_{34}y_3$ 的信号流图如下图所示。

步骤 4 - $y_5 = a_{45}y_4 + a_{35}y_3$ 的信号流图如下图所示。

步骤 5 - $y_6 = a_{56}y_5$ 的信号流图如下图所示。

步骤 6 - 整个系统的信号流图如下图所示。

将框图转换为信号流图
按照以下步骤将框图转换为其等效的信号流图。
将框图中的所有信号、变量、求和点和起飞点表示为信号流图中的节点。
将框图的块表示为信号流图中的分支。
将框图块内的传递函数表示为信号流图中分支的增益。
根据框图连接节点。如果两个节点之间存在连接(但中间没有块),则将该分支的增益表示为 1。例如,求和点之间、求和点与起飞点之间、输入与求和点之间、起飞点与输出之间。
例子
让我们将以下框图转换为其等效的信号流图。

将框图的输入信号$R(s)$和输出信号$C(s)$表示为信号流图的输入节点$R(s)$和输出节点$C(s)$。
仅供参考,其余节点(y 1至 y 9)在框图中进行了标记。除输入和输出节点外,还有九个节点。即四个节点用于四个求和点,四个节点用于四个起飞点,一个节点用于块 $G_1$ 和 $G_2$ 之间的变量。
下图显示了等效信号流图。

借助梅森增益公式(在下一章中讨论),您可以计算该信号流图的传递函数。这就是信号流图的优点。这里,我们不需要简化(简化)信号流图来计算传递函数。
梅森增益公式
现在让我们讨论梅森增益公式。假设信号流图中有“N”条前向路径。信号流图的输入和输出节点之间的增益只不过是系统的传递函数。可以利用梅森增益公式来计算。
梅森增益公式为
$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^N _{i=1}P_i\Delta _i}{\Delta}$$
在哪里,
C(s)是输出节点
R(s)是输入节点
T是 $R(s)$ 和 $C(s)$ 之间的传递函数或增益
P i是第 i 个前向路径增益
$\Delta =1-(所有\: 个体\: 循环\: 收益的总和)$
$+(所有可能的两个非接触循环的增益乘积之和)$
$$-(总和\:增益\:乘积\:所有\:可能\:三个\:非接触\:循环)+...$$
Δ i是通过去除与第 i个前向路径接触的环路而从 Δ 获得的。
请考虑以下信号流图,以了解此处涉及的基本术语。

小路
它是从一个节点按照分支箭头方向到任意其他节点的分支遍历。它不应多次遍历任何节点。
示例- $y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5$ 和 $y_5 \rightarrow y_3 \rightarrow y_2$
前进的道路
从输入节点到输出节点的路径称为前向路径。
示例- $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ 和 $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$。
前向路径增益
它是通过计算前向路径所有分支增益的乘积得到的。
示例- $abcde$ 是 $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$ 的前向路径增益,abge 是 $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow 的前向路径增益y_6$。
环形
从一个节点开始并在同一节点结束的路径称为循环。因此,它是一条封闭路径。
示例- $y_2 \rightarrow y_3 \rightarrow y_2$ 和 $y_3 \rightarrow y_5 \rightarrow y_3$。
环路增益
它是通过计算一个循环的所有分支增益的乘积而获得的。
示例- $b_j$ 是 $y_2 \rightarrow y_3 \rightarrow y_2$ 的环路增益,$g_h$ 是 $y_3 \rightarrow y_5 \rightarrow y_3$ 的环路增益。
非接触式循环
这些是循环,不应有任何公共节点。
示例- 循环 $y_2 \rightarrow y_3 \rightarrow y_2$ 和 $y_4 \rightarrow y_5 \rightarrow y_4$ 是非接触式的。
使用梅森增益公式计算传递函数
让我们考虑使用相同的信号流图来查找传递函数。

前向路径的数量,N = 2。
第一条前进路径是 - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_6$。
第一个前向路径增益,$p_1 = abcde$。
第二条前进路径是 - $y_1 \rightarrow y_2 \rightarrow y_3 \rightarrow y_5 \rightarrow y_6$。
第二个前向路径增益,$p_2 = abge$。
单独循环的数量,L = 5。
循环是 - $y_2 \rightarrow y_3 \rightarrow y_2$、$y_3 \rightarrow y_5 \rightarrow y_3$、$y_3 \rightarrow y_4 \rightarrow y_5 \rightarrow y_3$、$y_4 \rightarrow y_5 \rightarrow y_4$ 和 $y_5 \rightarrow y_5$。
循环增益为 - $l_1 = bj$、$l_2 = gh$、$l_3 = cdh$、$l_4 = di$ 和 $l_5 = f$。
两个非接触循环的数量 = 2。
第一个非接触循环对是 - $y_2 \rightarrow y_3 \rightarrow y_2$、$y_4 \rightarrow y_5 \rightarrow y_4$。
获得第一个非接触循环对的乘积,$l_1l_4 = bjdi$
第二个非接触循环对是 - $y_2 \rightarrow y_3 \rightarrow y_2$、$y_5 \rightarrow y_5$。
第二个非接触环路对的增益乘积为 - $l_1l_5 = bjf$
该信号流图中不存在更多数量(超过两个)的非接触环路。
我们知道,
$\Delta =1-(所有\: 个体\: 循环\: 收益的总和)$
$+(所有可能的两个非接触循环的增益乘积之和)$
$$-(总和\:增益\:乘积\:所有\:可能\:三个\:非接触\:循环)+...$$
代入上述方程中的值,
$\Delta =1-(bj+gh+cdh+di+f)+(bjdi+bjf)-(0)$
$\右箭头\Delta=1-(bj+gh+cdh+di+f)+bjdi+bjf$
不存在与第一条前向路径不接触的循环。
所以,$\Delta_1=1$。
类似地,$\Delta_2=1$。因为,没有与第二条前向路径不接触的循环。
代入梅森增益公式中的N = 2
$$T=\frac{C(s)}{R(s)}=\frac{\Sigma ^2 _{i=1}P_i\Delta _i}{\Delta}$$
$$T=\frac{C(s)}{R(s)}=\frac{P_1\Delta_1+P_2\Delta_2}{\Delta}$$
将所有必要的值代入上式中。
$$T=\frac{C(s)}{R(s)}=\frac{(abcde)1+(abge)1}{1-(bj+gh+cdh+di+f)+bjdi+bjf }$$
$$\Rightarrow T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf }$$
因此,传递函数是 -
$$T=\frac{C(s)}{R(s)}=\frac{(abcde)+(abge)}{1-(bj+gh+cdh+di+f)+bjdi+bjf}$ $
控制系统 - 时间响应分析
我们可以在时域和频域上分析控制系统的响应。我们将在后面的章节中讨论控制系统的频率响应分析。现在让我们讨论控制系统的时间响应分析。
什么是时间响应?
如果控制系统的输出随输入而变化,则称为控制系统的时间响应。时间响应由两部分组成。
- 瞬态响应
- 稳态响应
控制系统在时域的响应如下图所示。

这里,图中显示了瞬态和稳态。与这些状态相对应的响应称为瞬态响应和稳态响应。
在数学上,我们可以将时间响应 c(t) 写为
$$c(t)=c_{tr}(t)+c_{ss}(t)$$
在哪里,
- c tr (t) 是瞬态响应
- c ss (t) 是稳态响应
瞬态响应
将输入施加到控制系统后,输出需要一定的时间才能达到稳定状态。因此,输出将处于瞬态,直到达到稳态。因此,控制系统在瞬态期间的响应称为瞬态响应。
对于较大的“t”值,瞬态响应将为零。理想情况下,“t”的值是无穷大,实际上,它是常数的五倍。
从数学上来说,我们可以把它写成
$$\lim_{t\rightarrow \infty}c_{tr}(t)=0$$
稳态响应
即使在较大“t”值的瞬态响应为零值之后仍然保留的时间响应部分称为稳态响应。这意味着,即使在稳态期间,瞬态响应也将为零。
例子
让我们找到控制系统时间响应的瞬态和稳态项 $c(t)=10+5e^{-t}$
这里,第二项 $5e^{-t}$ 将为零,因为t表示无穷大。所以,这是瞬态术语。即使t接近无穷大,第一项 10 仍然存在。所以,这就是稳态项。
标准测试信号
标准测试信号有脉冲信号、阶跃信号、斜坡信号和抛物线信号。这些信号用于了解 p
