
- 控制系统教程
- 控制系统 - 主页
- 控制系统 - 简介
- 控制系统 - 反馈
- 数学模型
- 机械系统建模
- 机械系统的电气类比
- 控制系统 - 框图
- 框图代数
- 框图简化
- 信号流图
- 梅森增益公式
- 时间响应分析
- 一阶系统的响应
- 二阶系统响应
- 时域规格
- 稳态误差
- 控制系统 - 稳定性
- 控制系统 - 稳定性分析
- 控制系统 - 根轨迹
- 根轨迹的构建
- 频率响应分析
- 控制系统 - 波特图
- 波特图的构建
- 控制系统 - 极坐标图
- 控制系统 - 奈奎斯特图
- 控制系统 - 补偿器
- 控制系统 - 控制器
- 控制系统 - 状态空间模型
- 状态空间分析
- 控制系统有用的资源
- 控制系统 - 快速指南
- 控制系统 - 有用资源
- 控制系统 - 讨论
一阶系统的响应
在本章中,我们讨论一阶系统的时间响应。考虑以下闭环控制系统框图。这里,开环传递函数 $\frac{1}{sT}$ 与单位负反馈连接。
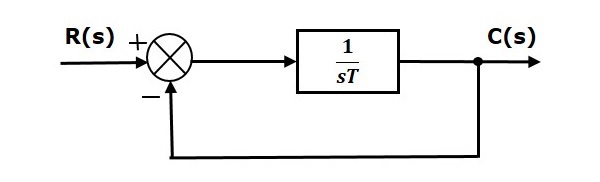
我们知道闭环控制系统的传递函数具有单位负反馈,
$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}$$
将 $G(s)=\frac{1}{sT}$ 代入上述方程中。
$$\frac{C(s)}{R(s)}=\frac{\frac{1}{sT}}{1+\frac{1}{sT}}=\frac{1}{sT+ 1}$$
s 的幂是分母项中的 1。因此,上述传递函数是一阶的,并且该系统被称为一阶系统。
我们可以将上面的等式重写为
$$C(s)=\left ( \frac{1}{sT+1} \right )R(s)$$
在哪里,
C(s)是输出信号 c(t) 的拉普拉斯变换,
R(s)是输入信号 r(t) 的拉普拉斯变换,并且
T是时间常数。
按照以下步骤获取一阶系统在时域中的响应(输出)。
对输入信号 $r(t)$ 进行拉普拉斯变换。
考虑方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
将 $R(s)$ 值代入上述方程中。
如果需要,计算 $C(s)$ 的部分分数。
对 $C(s)$ 应用拉普拉斯逆变换。
在上一章中,我们已经看到了脉冲、阶跃、斜坡和抛物线等标准测试信号。现在让我们逐一找出一阶系统对每个输入的响应。响应的名称根据输入信号的名称给出。例如,系统对脉冲输入的响应称为脉冲响应。
一阶系统的脉冲响应
将单位脉冲信号视为一阶系统的输入。
所以,$r(t)=\delta(t)$
在两侧应用拉普拉斯变换。
$R(s)=1$
考虑方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
将 $R(s) = 1$ 代入上式中。
$$C(s)=\left ( \frac{1}{sT+1} \right )(1)=\frac{1}{sT+1}$$
将上述方程重新排列为拉普拉斯变换的标准形式之一。
$$C(s)=\frac{1}{T\left (\ s+\frac{1}{T} \right )} \Rightarrow C(s)=\frac{1}{T}\left ( \压裂{1}{s+\压裂{1}{T}} \右)$$
在两侧应用拉普拉斯逆变换。
$$c(t)=\frac{1}{T}e^\left ( {-\frac{t}{T}} \right )u(t)$$
单位脉冲响应如下图所示。

单位脉冲响应c(t) 是“t”正值时的指数衰减信号,“t”负值时为零。
一阶系统的阶跃响应
将单位阶跃信号视为一阶系统的输入。
所以,$r(t)=u(t)$
在两侧应用拉普拉斯变换。
$$R(s)=\frac{1}{s}$$
考虑方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
将 $R(s)=\frac{1}{s}$ 代入上式中。
$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s} \right )=\frac{1}{s\left ( sT+ 1 \右)}$$
做 C(s) 的部分分数。
$$C(s)=\frac{1}{s\left ( sT+1 \right )}=\frac{A}{s}+\frac{B}{sT+1}$$
$$\Rightarrow \frac{1}{s\left ( sT+1 \right )}=\frac{A\left ( sT+1 \right )+Bs}{s\left ( sT+1 \right )} $$
两边的分母项相同。所以,他们会被彼此取消。因此,分子项相等。
$$1=A\左 ( sT+1 \右 )+Bs$$
将两边的常数项相等,即可得到 A = 1。
代入,A = 1 并使两边s项的系数相等。
$$0=T+B \右箭头 B=-T$$
将 A = 1 和 B = -T 代入 $C(s)$ 的部分分式展开式中。
$$C(s)=\frac{1}{s}-\frac{T}{sT+1}=\frac{1}{s}-\frac{T}{T\left ( s+\frac{ 1}{T} \右)}$$
$$\Rightarrow C(s)=\frac{1}{s}-\frac{1}{s+\frac{1}{T}}$$
在两侧应用拉普拉斯逆变换。
$$c(t)=\left ( 1-e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
单位阶跃响应c(t) 具有瞬态项和稳态项。
单位阶跃响应中的瞬态项是 -
$$c_{tr}(t)=-e^{-\left ( \frac{t}{T} \right )}u(t)$$
单位阶跃响应中的稳态项是 -
$$c_{ss}(t)=u(t)$$
下图显示了单位阶跃响应。

单位阶跃响应 c(t)的值在 t = 0 时为零并且对于 t 的所有负值。它从零值逐渐增加,最终达到稳定状态的一。因此,稳态值取决于输入的大小。
一阶系统的斜坡响应
将单位斜坡信号视为一阶系统的输入。
$所以,r(t)=tu(t)$
在两侧应用拉普拉斯变换。
$$R(s)=\frac{1}{s^2}$$
考虑方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
将 $R(s)=\frac{1}{s^2}$ 代入上述方程中。
$$C(s)=\left ( \frac{1}{sT+1} \right )\left ( \frac{1}{s^2} \right )=\frac{1}{s^2( ST+1)}$$
计算 $C(s)$ 的部分分数。
$$C(s)=\frac{1}{s^2(sT+1)}=\frac{A}{s^2}+\frac{B}{s}+\frac{C}{sT +1}$$
$$\Rightarrow \frac{1}{s^2(sT+1)}=\frac{A(sT+1)+Bs(sT+1)+Cs^2}{s^2(sT+1) }$$
两边的分母项相同。所以,他们会被彼此取消。因此,分子项相等。
$$1=A(sT+1)+Bs(sT+1)+Cs^2$$
将两边的常数项相等,即可得到 A = 1。
代入,A = 1 并使两边 s 项的系数相等。
$$0=T+B \右箭头 B=-T$$
类似地,代入 B = −T 并使两边 $s^2$ 项的系数相等。您将得到$C=T^2$。
将 A = 1、B = −T 和 $C = T^2$ 代入 $C(s)$ 的部分分式展开式中。
$$C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T^2}{sT+1}=\frac{1}{s^2} -\frac{T}{s}+\frac{T^2}{T\left ( s+\frac{1}{T} \right )}$$
$$\Rightarrow C(s)=\frac{1}{s^2}-\frac{T}{s}+\frac{T}{s+\frac{1}{T}}$$
在两侧应用拉普拉斯逆变换。
$$c(t)=\left ( t-T+Te^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
单位斜坡响应c(t) 具有瞬态项和稳态项。
单位斜坡响应中的瞬态项是 -
$$c_{tr}(t)=Te^{-\left ( \frac{t}{T} \right )}u(t)$$
单位斜坡响应中的稳态项是 -
$$c_{ss}(t)=(tT)u(t)$$
下图显示了单位斜坡响应。

对于 t 的所有正值,单位斜坡响应 c(t) 遵循单位斜坡输入信号。但是,输入信号存在 T 个单位的偏差。
一阶系统的抛物线响应
将单位抛物线信号视为一阶系统的输入。
所以,$r(t)=\frac{t^2}{2}u(t)$
在两侧应用拉普拉斯变换。
$$R(s)=\frac{1}{s^3}$$
考虑方程 $C(s)=\left ( \frac{1}{sT+1} \right )R(s)$
将 $R(s)=\frac{1}{s^3}$ 代入上式中。
$$C(s)=\left ( \frac{1}{sT+1} \right )\left( \frac{1}{s^3} \right )=\frac{1}{s^3( ST+1)}$$
计算 $C(s)$ 的部分分数。
$$C(s)=\frac{1}{s^3(sT+1)}=\frac{A}{s^3}+\frac{B}{s^2}+\frac{C} {s}+\frac{D}{sT+1}$$
化简后,A、B、C、D 的值分别为 1、$-T、\: T^2\: 和 \: −T^3$。将这些值代入上述 C(s) 的部分分数展开式中。
$C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^3}{sT+1 } \: \Rightarrow C(s)=\frac{1}{s^3}-\frac{T}{s^2}+\frac{T^2}{s}-\frac{T^2} {s+\frac{1}{T}}$
在两侧应用拉普拉斯逆变换。
$$c(t)=\left ( \frac{t^2}{2} -Tt+T^2-T^2e^{-\left ( \frac{t}{T} \right )} \right )u(t)$$
单位抛物线响应c(t) 具有瞬态项和稳态项。
单位抛物线响应中的瞬态项是
$$C_{tr}(t)=-T^2e^{-\left ( \frac{t}{T} \right )}u(t)$$
单位抛物线响应中的稳态项是
$$C_{ss}(t)=\left ( \frac{t^2}{2} -Tt+T^2 \right )u(t)$$
从这些响应中,我们可以得出结论,一阶控制系统对于斜坡和抛物线输入并不稳定,因为这些响应即使在无限长的时间内也会继续增加。一阶控制系统对于脉冲和阶跃输入是稳定的,因为这些响应具有有界输出。但是,脉冲响应没有稳态项。因此,阶跃信号在时域中被广泛使用,用于根据控制系统的响应来分析控制系统。
