使用 Excel 求解器进行优化

Solver是一个 Microsoft Excel 插件程序，可用于假设分析中的优化。

根据 O'Brien 和 Marakas 的说法，优化分析是目标寻求分析的更复杂的扩展。我们的目标不是为变量设置特定的目标值，而是在某些约束下找到一个或多个目标变量的最佳值。然后，根据指定的约束，重复更改一个或多个其他变量，直到发现目标变量的最佳值。

在 Excel 中，您可以使用规划求解在工作表上其他公式单元格的值的特定约束或限制下，在称为目标单元格的一个单元格中查找公式的最佳值（最大值或最小值，或某个值）。

这意味着求解器使用一组称为决策变量的单元格，这些变量用于计算目标单元格和约束单元格中的公式。求解器调整决策变量单元格中的值以满足约束单元格的限制并为目标单元格生成所需的结果。

您可以使用 Solver 来找到各种问题的最佳解决方案，例如 -

确定药品生产单位的每月产品组合，以实现利润最大化。
安排组织中的劳动力。
解决交通问题。
财务规划和预算。

激活求解器插件

在继续使用 Solver 寻找问题的解决方案之前，请确保在 Excel 中激活Solver 插件，如下所示 -

单击功能区上的数据选项卡。Solver命令应出现在 Analysis 组中，如下所示。

如果您没有找到 Solver 命令，请按如下方式激活它 -

单击“文件”选项卡。
单击左侧窗格中的选项。出现 Excel 选项对话框。
单击左侧窗格中的加载项。
在“管理”框中选择“Excel 加载项”，然后单击“前往”。

将出现“加载项”对话框。选中Solver Add-in并单击“确定”。现在，您应该能够在功能区的“数据”选项卡下找到“求解器”命令。

Solver 使用的求解方法

您可以根据问题的类型选择 Excel Solver 支持的以下三种求解方法之一 -

LP单纯形

用于线性问题。求解器模型在以下条件下是线性的 -

通过将（变化单元格）*（常量）形式的项加在一起来计算目标单元格。
每个约束都满足线性模型要求。这意味着通过将（变化的单元格）*（常数）形式的项加在一起并将总和与常数进行比较来评估每个约束。

广义降梯度 (GRG) 非线性

用于平滑非线性问题。如果您的目标单元格、任何约束或两者都包含对不属于（变化单元格）*（常量）形式的变化单元格的引用，则您有一个非线性模型。

进化论

了解求解器评估

求解器需要以下参数 -

决策可变单元
约束单元
目标细胞
解法

求解器评估基于以下内容 -

决策变量单元格中的值受到约束单元格中的值的限制。
目标单元格中的值的计算包括决策变量单元格中的值。
求解器使用所选的求解方法来产生目标单元中的最优值。

定义问题

假设您正在分析一家制造和销售某种产品的公司所获得的利润。要求您找出未来两个季度可以用于广告的金额，上限为 20,000。每个季度的广告水平影响以下因素 -

销售的单位数量，间接决定销售收入的数额。
相关费用，以及
利润。

您可以继续将问题定义为 -

求单位成本。
找出每单位的广告费用。
查找单价。

接下来，设置所需计算的单元格，如下所示。

正如您所观察到的，对第 1 季度和第 2 季度进行的计算是 -

第一季度可供销售的单位数量为 400 个，第二季度为 600 个（单元格 - C7 和 D7）。
广告预算的初始值设置为每季度 10000（单元格 - C8 和 D8）。
销售单位数量取决于每单位的广告成本，因此是季度/广告的预算。每单位成本。请注意，我们使用了 Min 函数来注意查看 no。售出的单位数量 <= 数量可用单位数。（细胞 - C9 和 D9）。
收入的计算方式为单价 * 销售数量（电池 – C10 和 D10）。
费用计算公式为：单位成本 * 可用单位数量 + 广告费用。该季度的成本（单元 - C11 和 D12）。
利润是收入 – 费用（单元格 C12 和 D12）。
总利润为第 1 季度的利润 + 第 2 季度的利润（单元格 - D3）。

接下来，您可以设置求解器的参数，如下所示 -

正如您所观察到的，求解器的参数是 -

目标单元格是 D3，其中包含您想要最大化的总利润。
决策变量单元格是 C8 和 D8，其中包含两个季度（第 1 季度和第 2 季度）的预算。
共有三个约束单元 - C14、C15 和 C16。
- 包含总预算的单元格 C14 将设置约束 20000（单元格 D14）。
- 单元格 C15 包含编号。第 1 季度销售的单位数量是设置 <= no 的约束。第一季度可用单位数（单元格 D15）。
- 单元格 C16 包含编号。第二季度销售的单位数量是设置 <= no 的约束。第二季度可用单位数（单元格 D16）。

解决问题

下一步是使用 Solver 来找到解决方案，如下所示 -

步骤 1 - 转到功能区上的数据 > 分析 > 求解器。将出现“求解器参数”对话框。

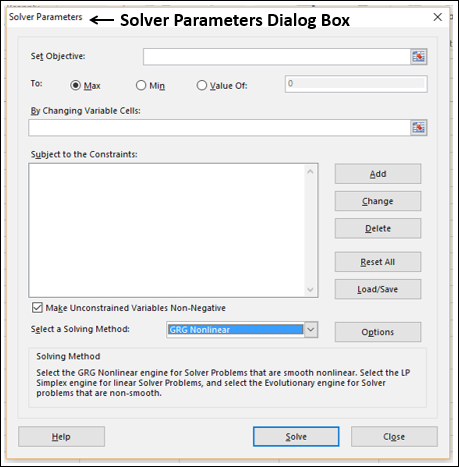
步骤 2 - 在“设置目标”框中，选择单元格 D3。

步骤 3 - 选择最大。

步骤 4 - 在“通过更改变量单元格”框中选择范围 C8:D8 。

步骤 5 - 接下来，单击“添加”按钮添加您已确定的三个约束。

步骤 6 - 将出现“添加约束”对话框。如下所示设置总预算的约束，然后单击“添加”。

步骤 7 - 设置总数的约束。第 1 季度销售的单位数量如下所示，然后单击“添加”。

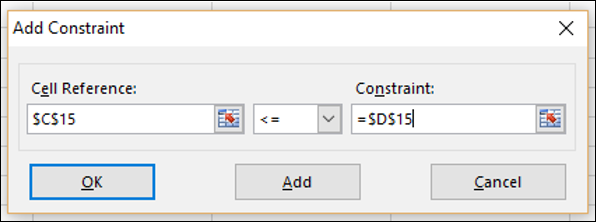
步骤 8 - 设置总数的约束。第二季度销售的单位数如下所示，然后单击“确定”。

将出现“求解器参数”对话框，其中添加了三个约束 -“受约束”框。

步骤 9 - 在选择求解方法框中，选择单纯形 LP。

步骤 10 - 单击“求解”按钮。将出现求解器结果对话框。选择保留求解器解并单击确定。

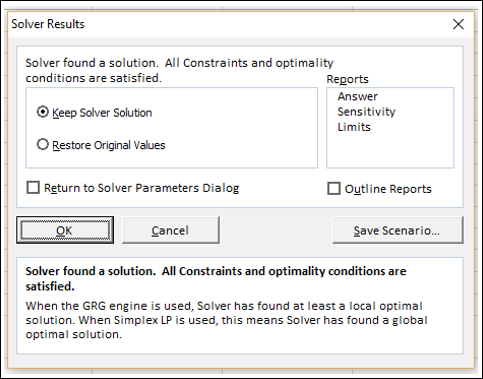
结果将显示在您的工作表中。

正如您所观察到的，在给定的约束条件下，产生最大总利润的最佳解决方案如下：

总利润 – 30000。
副词。第一季度预算 – 8000。
副词。第二季度预算 – 12000。

逐步完成求解器试验解决方案

您可以逐步完成求解器试验解决方案，查看迭代结果。

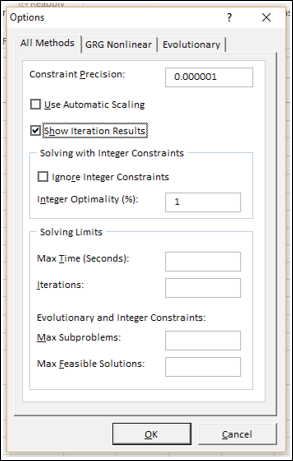
步骤 1 - 单击“求解器参数”对话框中的“选项”按钮。

将出现“选项”对话框。

步骤 2 - 选择“显示迭代结果”框并单击“确定”。

步骤 3 -出现求解器参数对话框。单击“求解”。

步骤 4 -出现“显示试验解决方案”对话框，显示消息 -求解器已暂停，当前解决方案值显示在工作表上。

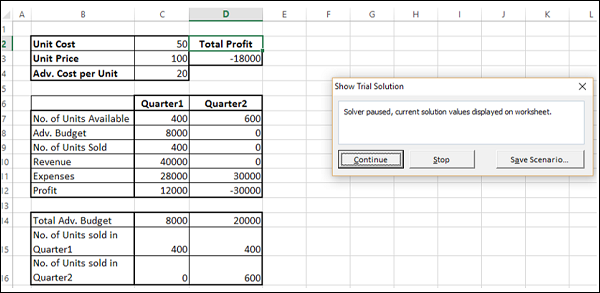
正如您所观察到的，当前迭代值显示在您的工作单元中。您可以停止求解器接受当前结果，也可以继续使用求解器在后续步骤中寻找解。

步骤 5 - 单击继续。

每一步都会出现“显示试验解决方案”对话框，最后找到最佳解决方案后，会出现“规划求解结果”对话框。您的工作表在每一步都会更新，最终显示结果值。

保存解算器选择

对于使用 Solver 解决的问题，您有以下保存选项 -

您可以通过保存工作簿将“求解器参数”对话框中的最后选择与工作表一起保存。
工作簿中的每个工作表都可以有自己的求解器选择，并且在保存工作簿时所有这些都将被保存。
您还可以在工作表中定义多个问题，每个问题都有自己的求解器选择。在这种情况下，您可以使用“求解器参数”对话框中的“加载/保存”单独加载和保存问题。
- 单击加载/保存按钮。将出现“加载/保存”对话框。
- 要保存问题模型，请输入要在其中放置问题模型的垂直空单元格范围的第一个单元格的引用。单击“保存”。

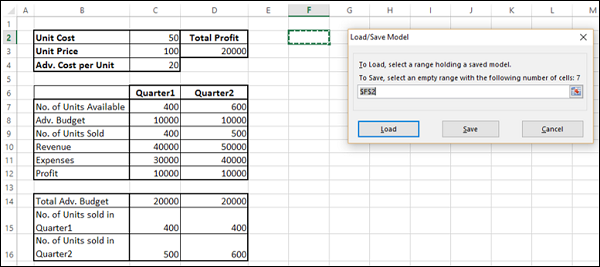
问题模型（求解器参数集）从您作为参考给出的单元格开始显示。

要加载问题模型，请输入包含问题模型的整个单元格范围的引用。然后，单击“加载”按钮。