Excel数据财务分析

您可以轻松地使用 Excel 进行财务分析。Excel为您提供了PMT、PV、NPV、XNPV、IRR、MIRR、XIRR等多种财务函数，使您能够快速得出财务分析结果。

在本章中，您将了解在何处以及如何使用这些函数进行分析。

什么是年金？

年金是在连续时期内支付的一系列恒定现金。例如，退休储蓄、保险付款、住房贷款、抵押贷款等。在年金函数中 -

正数代表收到的现金。
负数代表支付的现金。

一系列未来付款的现值

现值是一系列未来付款现在价值的总和。您可以使用 Excel 函数计算现值 -

PV - 通过使用利率和一系列未来付款（负值）和收入（正值）来计算投资的现值。至少其中一项现金流必须为正，至少一项必须为负。
NPV - 通过使用贴现率和一系列定期未来付款（负值）和收入（正值）来计算投资的净现值。
XNPV - 计算不一定是周期性的现金流表的净现值。

请注意-

PV 现金流量必须恒定，而 NPV 现金流量可以是可变的。
PV 现金流量可以在期初或期末，而 NPV 现金流量必须在期末。
NPV 现金流量必须是周期性的，而 XNPV 现金流量不必是周期性的。

在本节中，您将了解如何使用 PV。您将在后面的部分中了解 NPV。

例子

假设您要购买一台冰箱。销售人员告诉你，冰箱的价格是32000，但是你可以选择分8年付清，年利率13%，每年还款6000。你也可以选择分期付款每年年初或年底。

您想知道这些选项中哪一个对您有利。

您可以使用 Excel 函数 PV -

PV (rate, nper, pmt, [fv ], [type])

要计算每年年底付款的现值，请省略类型或为类型指定 0。

要计算每年年底付款的现值，请为类型指定 1。

您将得到以下结果 -

所以，

如果现在付款，则需要支付现值32000。
如果您选择按年付款并在年底付款，则需要支付现值 28, 793。
如果您选择按年付款并在年底付款，则需要支付现值32,536。

您可以清楚地看到选项 2 对您有利。

什么是电磁干扰？

Investopedia 将等值月供 (EMI) 定义为“借款人在每个日历月的指定日期向贷方支付的固定付款金额。等值月供用于每月还清利息和本金，以便超过在指定的年限内，贷款将全额还清。”

EMI 贷款

在 Excel 中，您可以使用 PMT 函数计算贷款的 EMI。

假设您想申请一笔500万的住房贷款，年利率为11.5%，贷款期限为25年。您可以按如下方式找到您的 EMI -

计算每月利率（年利率/12）
计算每月还款次数（年数*12）
使用PMT函数计算EMI

正如你所观察到的，

现值 (PV) 是贷款金额。
终值 (FV) 为 0，因为在期限结束时贷款金额应为 0。
类型为 1，因为 EMI 在每个月初支付。

您将得到以下结果 -

每月偿还贷款本金和利息

EMI包括利息和部分本金的支付。随着时间的增加，这两个 EMI 分量会发生变化，从而降低平衡度。

要得到

您每月还款的利息部分，您可以使用Excel IPMT 函数。
您每月付款的本金部分的支付，您可以使用Excel PPMT 功能。

例如，如果您以 16% 的年利率申请了 1,000,000 美元的贷款，期限为 8 个月。您可以获得 8 个月内的 EMI 值、减少的利息金额、增加的本金支付额以及减少的贷款余额。8个月末，贷款余额为0。

请按照下面给出的步骤进行操作。

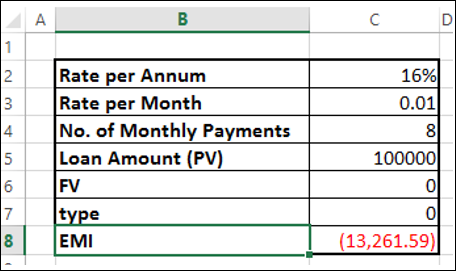
步骤 1 - 按如下方式计算 EMI。

这导致 EMI 为 Rs。13261.59。

步骤 2 - 接下来计算 8 个月的 EMI 的利息和本金部分，如下所示。

您将得到以下结果。

两个期间之间支付的利息和本金

您可以计算两个期间（含）之间支付的利息和本金。

使用 CUMIPMT 函数计算第 2^个月和第 3^个月之间支付的累积利息。
^{验证第 2个}月和第 3^个月利息值的总和结果。
使用 CUMPRINC 函数计算第 2^个月和第 3^个月之间支付的累积本金。
^{验证第 2个}月和第 3^个月主值的总和结果。

您将得到以下结果。

您可以看到您的计算与验证结果相符。

计算利率

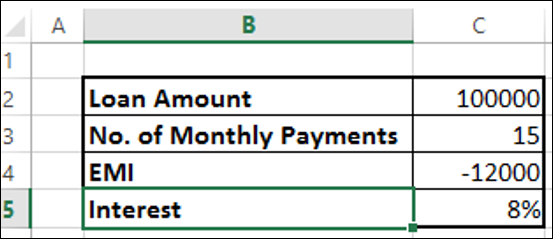
假设您借了 100,000 美元的贷款，并且希望在 15 个月内还款，每月最高还款额为 12000 美元。您可能想知道必须支付的利率。

使用 Excel RATE 函数查找利率 -

您将得到 8% 的结果。

计算贷款期限

假设您以 10% 的利率借了 100,000 美元的贷款。您希望每月最高还款额为 15,000 美元。您可能想知道还清贷款需要多长时间。

使用 Excel NPER 函数查找付款次数

12 个月后您将得到结果。

投资决策

当您想要进行投资时，您会比较不同的选择并选择能产生更好回报的选择。净现值可用于比较一段时间内的现金流并确定哪一个更好。现金流可以定期、定期或不定期发生。

首先，我们考虑定期现金流量的情况。

从现在起 n 年内（n 可以是分数）在不同时间点收到的一系列现金流的净现值为1/(1 + r) ⁿ，其中 r 是年利率。

考虑以下两项为期三年的投资。

从表面上看，投资 1 看起来比投资 2 更好。但是，只有当您了解当前投资的真正价值时，您才能决定哪种投资更好。您可以使用 NPV 函数来计算回报。

现金流可能会发生

每年年底的时候。
每年年初的时候。
每年中旬的时候。

NPV 函数假设现金流量为年末。如果现金流发生在不同时间，那么您必须在计算 NPV 的同时考虑该特定因素。

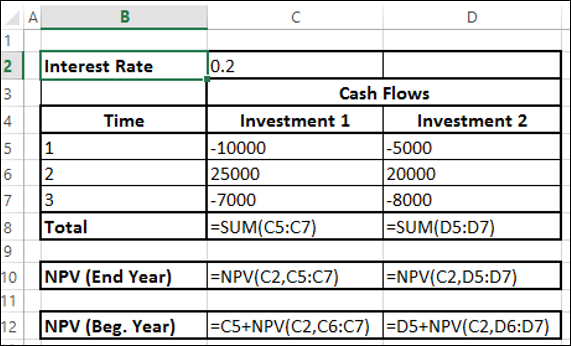
假设现金流量发生在年底。然后您就可以直接使用 NPV 功能。

您将得到以下结果 -

正如您所观察到的，投资 2 的 NPV 高于投资 1。因此，投资 2 是更好的选择。您得到此结果是因为与投资 1 相比，投资 2 的现金流出处于较晚的时期。

年初现金流量

假设现金流发生在每年年初。在这种情况下，您不应将第一现金流量纳入 NPV 计算中，因为它已经代表当前值。您需要将第一个现金流量添加到从其余现金流量获得的净现值中以获得净现值。

您将得到以下结果 -

年中现金流

假设现金流发生在每年年中。在这种情况下，您需要将从现金流中获得的 NPV 乘以 $\sqrt{1+r}$ 以获得净现值。

您将得到以下结果 -

不定期现金流量

如果要计算不规则现金流（即随机时间发生的现金流）的净现值，则计算有点复杂。

然而，在Excel中，您可以使用XNPV函数轻松地进行这样的计算。

将您的数据与日期和现金流量一起排列。

注意- 数据中的第一个日期应该是所有日期中最早的日期。其他日期可以按任何顺序出现。

使用 XNPV 函数计算净现值。

您将得到以下结果 -

假设今天的日期是 2015 年 3 月 15 日^。正如您所观察到的，所有现金流量的日期都是较晚的日期。如果您想查找截至今天的净现值，请将其包含在顶部的数据中，并为现金流指定 0。

您将得到以下结果 -

内部回报率 (IRR)

投资的内部收益率 (IRR) 是 NPV 为 0 时的利率。它是正现金流量的现值恰好补偿负现金流量的利率值。当贴现率为IRR时，投资是完全无关的，即投资者既不赚钱也不赔钱。

考虑以下现金流、不同的利率和相应的 NPV 值。

正如您所观察到的，利率值在 10% 和 11% 之间，NPV 的符号会发生变化。当您将利率微调至 10.53% 时，NPV 接近于 0。因此，IRR 为 10.53%。

确定项目现金流量的 IRR

您可以使用 Excel 函数 IRR 计算现金流量的 IRR。

正如您在上一节中看到的，IRR 为 10.53%。

对于给定的现金流量，IRR 可能 -

存在且唯一
存在且多个
不存在

独特的内部收益率

如果IRR存在并且是唯一的，它可以用来在几种可能性中选择最好的投资。

如果第一笔现金流为负，说明投资者有钱，想要投资。那么，IRR 越高越好，因为它代表投资者收到的利率。
如果第一笔现金流为正，则意味着投资者需要资金并正在寻求贷款，IRR 越低越好，因为它代表投资者支付的利率。

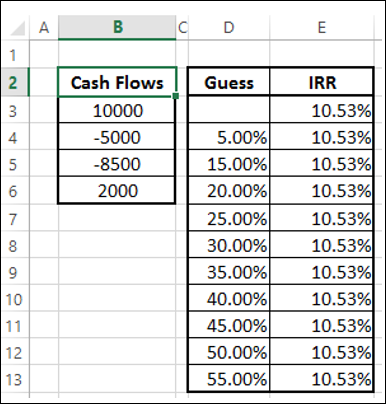
要确定 IRR 是否唯一，请改变猜测值并计算 IRR。如果 IRR 保持不变，那么它是唯一的。

正如您所观察到的，对于不同的猜测值，IRR 具有唯一的值。

多重IRR

在某些情况下，您可能有多个 IRR。考虑以下现金流量。使用不同的猜测值计算 IRR。

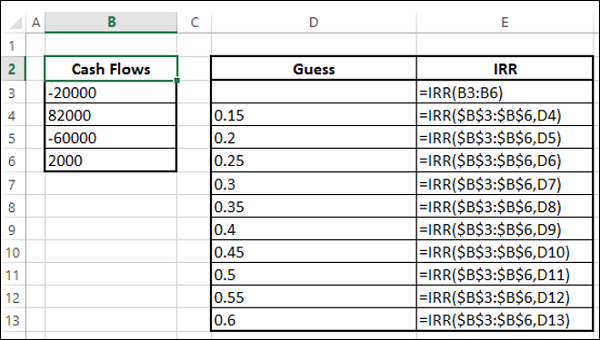
您将得到以下结果 -

您可以观察到有两个 IRR - -9.59% 和 216.09%。您可以验证这两个 IRR 计算 NPV。

对于 -9.59% 和 216.09%，NPV 均为 0。

无内部收益率

在某些情况下，您可能没有 IRR。考虑以下现金流量。使用不同的猜测值计算 IRR。

您将得到所有猜测值的#NUM 结果。

结果#NUM 表示所考虑的现金流没有 IRR。

现金流量模式和 IRR

如果现金流量只有一个符号变化，例如从负值变为正值或从正值变为负值，则可以保证获得唯一的 IRR。例如，在资本投资中，第一个现金流将为负，而其余现金流将为正。在这种情况下，存在独特的 IRR。

如果现金流量出现多个符号变化，IRR 可能不存在。即使存在，也可能不是唯一的。

基于 IRR 的决策

许多分析师更喜欢使用 IRR，它是一种流行的盈利能力衡量标准，因为以百分比形式表示，它很容易理解，也很容易与所需回报进行比较。然而，利用 IRR 进行决策时存在一些问题。如果您根据 IRR 进行排名并根据这些排名做出决策，您最终可能会做出错误的决策。

您已经看到 NPV 将使您能够做出财务决策。然而，当项目相互排斥时，IRR 和 NPV 并不总是会导致相同的决策。

互斥项目是指选择一个项目而无法接受另一个项目的项目。当比较的项目相互排斥时，NPV 和 IRR 之间可能会出现排名冲突。如果您必须在项目 A 和项目 B 之间进行选择，NPV 可能会建议接受项目 A，而 IRR 可能会建议项目 B。

NPV 和 IRR 之间的这种冲突可能是由于以下原因之一引起的 -

这些项目的规模差异很大，或者
现金流的时间不同。

规模差异显着的项目

如果你想用IRR来做决策，项目A的回报率为100，项目B的回报率为50。因此，项目A的投资看起来是有利可图的。然而，由于项目规模的差异，这是一个错误的决定。

考虑 -

你有1000可以投资。
如果您在项目 A 上投资 1000 美元，您将获得 100 美元的回报。
如果你在项目 B 上投资 100，你手里还有 900 可以投资到另一个项目，比如项目 C。假设你在项目 C 上获得 20% 的回报，那么项目 B 和项目 C 的总回报为230，在盈利能力方面遥遥领先。

因此，在这种情况下，净现值是一种更好的决策方法。

具有不同现金流时间的项目

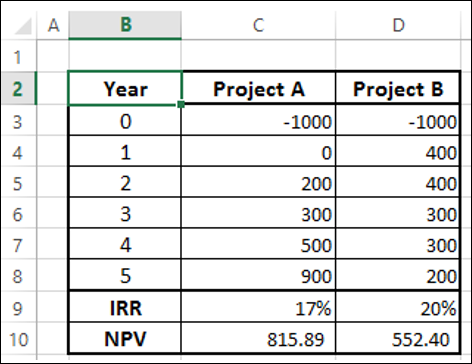
同样，如果您考虑 IRR 来决定，项目 B 将是您的选择。然而，项目A的NPV较高，是一个理想的选择。

不规则分布现金流的 IRR (XIRR)

您的现金流有时可能不规则。在这种情况下，您不能使用 IRR，因为 IRR 需要相等的时间间隔。您可以使用 XIRR，它会考虑现金流量的日期和现金流量。

得出的内部回报率为 26.42%。

修正内部收益率 (MIRR)

考虑您的财务利率与再投资利率不同的情况。如果您用 IRR 计算内部收益率，则假定融资和再投资的利率相同。此外，您还可能获得多个 IRR。

例如，考虑下面给出的现金流量 -

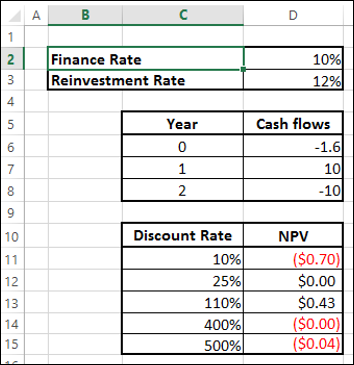
正如您所观察到的，NPV 多次为 0，从而导致多个 IRR。此外，不考虑再投资率。在这种情况下，您可以使用修改后的 IRR (MIRR)。

您将得到 7% 的结果，如下所示 -

注意- 与 IRR 不同，MIRR 始终是唯一的。