DSP - Z 变换属性
在本章中,我们将了解 Z 变换的基本属性。
线性度
它指出,当两个或多个单独的离散信号乘以常数时,它们各自的 Z 变换也将乘以相同的常数。
从数学上来说,
$$a_1x_1(n)+a_2x_2(n) = a_1X_1(z)+a_2X_2(z)$$证明- 我们知道,
$$X(Z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$$$= \sum_{n=-\infty}^\infty (a_1x_1(n)+a_2x_2(n))Z^{-n}$
$= a_1\sum_{n = -\infty}^\infty x_1(n)Z^{-n}+a_2\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$
$= a_1X_1(z)+a_2X_2(z)$ (由此证明)
这里,ROC 是 $ROC_1\bigcap ROC_2$。
时移
时移特性描述了离散信号在时域的变化如何影响Z域,可以写为:
$$x(n-n_0)\longleftrightarrow X(Z)Z^{-n}$$或$x(n-1)\longleftrightarrow Z^{-1}X(Z)$
证明-
令$y(P) = X(PK)$
$Y(z) = \sum_{p = -\infty}^\infty y(p)Z^{-p}$
$= \sum_{p = -\infty}^\infty (x(pk))Z^{-p}$
令 s = pk
$= \sum_{s = -\infty}^\infty x(s)Z^{-(s+k)}$
$= \sum_{s = -\infty}^\infty x(s)Z^{-s}Z^{-k}$
$= Z^{-k}[\sum_{s=-\infty}^\infty x(m)Z^{-s}]$
$= Z^{-k}X(Z)$ (由此证明)
这里,ROC 可以写为 Z = 0 (p>0) 或 Z = ∞(p<0)
例子
U(n) 和 U(n-1) 可以绘制如下
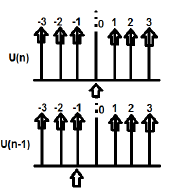
U(n) 的 Z 变换可写为:
$\sum_{n = -\infty}^\infty [U(n)]Z^{-n} = 1$
U(n-1) 的 Z 变换可以写为:
$\sum_{n = -\infty}^\infty [U(n-1)]Z^{-n} = Z^{-1}$
所以这里 $x(n-n_0) = Z^{-n_0}X(Z)$ (因此证明)
时间缩放
时间缩放属性告诉我们,当时间以离散形式缩放时,信号的 Z 域是什么,可以写为:
$$a^nx(n) \longleftrightarrow X(a^{-1}Z)$$证明-
令$y(p) = a^{p}x(p)$
$Y(P) = \sum_{p=-\infty}^\infty y(p)Z^{-p}$
$= \sum_{p=-\infty}^\infty a^px(p)Z^{-p}$
$= \sum_{p=-\infty}^\infty x(p)[a^{-1}Z]^{-p}$
$= X(a^{-1}Z)$ (由此证明)
ROC:= Mod(ar1) < Mod(Z) < Mod(ar2) 其中 Mod = 模
例子
让我们使用时间缩放属性来确定 $x(n) = a^n \cos \omega n$ 的 Z 变换。
解决方案-
我们已经知道信号 $\cos (\omega n)$ 的 Z 变换由下式给出 -
$$\sum_{n=-\infty}^\infty(\cos \omega n)Z^{-n} = (Z^2-Z \cos \omega)/(Z^2-2Z\cos \omega +1)$$
现在,应用时间缩放属性,$a^n \cos \omega n$ 的 Z 变换可以写为:
$\sum_{n=-\infty}^\infty(a^n\cos \omega n)Z^{-n} = X(a^{-1}Z)$
$= [(a^{-1}Z)^2-(a^{-1}Z \cos \omega n)]/((a^{-1}Z)^2-2(a^{- 1}Z \cos \omega n)+1)$
$= Z(Za \cos \omega)/(Z^2-2az \cos \omega+a^2)$
连续分化
连续微分性质表明,当我们在时域中对离散信号相对于时间进行微分时,将会发生 Z 变换。如下所示。
$$\frac{dx(n)}{dn} = (1-Z^{-1})X(Z)$$证明-
考虑方程的 LHS − $\frac{dx(n)}{dn}$
$$= \frac{[x(n)-x(n-1)]}{[n-(n-1)]}$$$= x(n)-X(n-1)$
$= x(Z)-Z^{-1}x(Z)$
$= (1-Z^{-1})x(Z)$ (由此证明)
ROC:R1< Mod (Z) <R2
例子
让我们求 $x(n) = n^2u(n)$ 给出的信号的 Z 变换
根据属性我们可以写
$Zz[nU(n)] = -Z\frac{dZ[U(n)]}{dz}$
$= -Z\frac{d[\frac{Z}{Z-1}]}{dZ}$
$= Z/((Z-1)^2$
$= y(让)$
现在,通过再次应用该属性可以找到 Z[ny],
$Z(n,y) = -Z\frac{dy}{dz}$
$= -Z\frac{d[Z/(Z-1)^3]}{dz}$
$= Z(Z+1)/(Z-1)^2$
卷积
这描述了当卷积以离散信号形式发生时系统 Z 域的变化,可以写为 -
$x_1(n)*x_2(n) \longleftrightarrow X_1(Z).X_2(Z)$
证明-
$X(Z) = \sum_{n = -\infty}^\infty x(n)Z^{-n}$
$= \sum_{n=-\infty}^\infty[\sum_{k = -\infty}^\infty x_1(k)x_2(nk)]Z^{-n}$
$= \sum_{k = -\infty}^\infty x_1(k)[\sum_n^\infty x_2(nk)Z^{-n}]$
$= \sum_{k = -\infty}^\infty x_1(k)[\sum_{n = -\infty}^\infty x_2(nk)Z^{-(nk)}Z^{-k}] $
设 nk = l,则上式可写为 -
$X(Z) = \sum_{k = -\infty}^\infty x_1(k)[Z^{-k}\sum_{l=-\infty}^\infty x_2(l)Z^{-l }]$
$= \sum_{k = -\infty}^\infty x_1(k)X_2(Z)Z^{-k}$
$= X_2(Z)\sum_{k = -\infty}^\infty x_1(Z)Z^{-k}$
$= X_1(Z).X_2(Z)$ (由此证明)
ROC:$ROC\大盘 ROC2$
例子
让我们找到两个信号给出的卷积
$x_1(n) = \lbrace 3,-2,2\rbrace$ ...(eq. 1)
$x_2(n) = \lbrace 2,0\leq 4\quad 和\quad 0\quad 其他地方\rbrace$ ...(eq. 2)
第一个方程的 Z 变换可以写为:
$\sum_{n = -\infty}^\infty x_1(n)Z^{-n}$
$= 3-2Z^{-1}+2Z^{-2}$
第二信号的 Z 变换可以写为:
$\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$
$= 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$
因此,上述两个信号的卷积由下式给出 -
$X(Z) = [x_1(Z)^*x_2(Z)]$
$= [3-2Z^{-1}+2Z^{-2}]\times [2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4 }]$
$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+...\四元...\四元...$
进行 Z 逆变换,我们得到:
$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$
初值定理
如果x(n)是因果序列,其Z变换为X(z),则初值定理可以写为:
$X(n)(at\quad n = 0) = \lim_{z \to \infty} X(z)$
证明- 我们知道,
$X(Z) = \sum_{n = 0} ^\infty x(n)Z^{-n}$
将上面的级数展开,我们得到;
$= X(0)Z^0+X(1)Z^{-1}+X(2)Z^{-2}+...\四元...$
$= X(0)\times 1+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$
在上述情况下,如果 Z → ∞ 则 $Z^{-n}\rightarrow 0$ (因为 n>0)
因此,我们可以说;
$\lim_{z \to \infty}X(z) = X(0)$ (由此证明)
最终值定理
最终值定理指出,如果信号的 Z 变换表示为 X(Z) 并且极点都在圆内,则其最终值表示为 x(n) 或 X(∞) 并且可以写为-
$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$
条件-
- 它仅适用于因果系统。
- $X(Z)(1-Z^{-1})$ 的极点应位于 Z 平面的单位圆内。
证明- 我们知道
$Z^+[x(n+1)-x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x (n)]$
$\Rightarrow Z^+[x(n+1)]-Z^+[x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x (n+1)-x(n)]$
$\Rightarrow Z[X(Z)^+-x(0)]-X(Z)^+ = \lim_{k \to \infty}\sum_{n = 0}^kZ^{-n}[x (n+1)-x(n)]$
在这里,我们可以应用单边 Z 变换的高级属性。因此,上式可以重写为:
$Z^+[x(n+1)] = Z[X(2)^+-x(0)Z^0] = Z[X(Z)^+-x(0)]$
现在将 z = 1 代入上式,我们可以展开上式 -
$\lim_{k \to \infty}{[x(1)-x(0)+x(6)-x(1)+x(3)-x(2)+...\quad... \quad...+x(x+1)-x(k)]}$
这可以表述为:
$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$ (由此证明)
例子
让我们找到 x(n) 的初始值和最终值,其信号由下式给出
$X(Z) = 2+3Z^{-1}+4Z^{-2}$
解决方案- 首先,通过应用定理找到信号的初始值
$x(0) = \lim_{z \到 \infty}X(Z)$
$= \lim_{z \到 \infty}[2+3Z^{-1}+4Z^{-2}]$
$= 2+(\frac{3}{\infty})+(\frac{4}{\infty}) = 2$
现在让我们应用定理找到信号的最终值
$x(\infty) = \lim_{z \to \infty}[(1-Z^{-1})X(Z)]$
$= \lim_{z \to \infty}[(1-Z^{-1})(2+3Z^{-1}+4Z^{-2})]$
$= \lim_{z \到 \infty}[2+Z^{-1}+Z^{-2}-4Z^{-3}]$
$= 2+1+1-4 = 0$
下面列出了 Z 变换的一些其他属性-
频率微分
当离散信号相对于时间微分时,它给出了信号 Z 域的变化。
$nx(n)\longleftrightarrow -Z\frac{dX(z)}{dz}$
其ROC可写为;
$r_2< Mod(Z)< r_1$
例子
让我们通过频率微分求出 x(n) 的值,其 Z 域中的离散信号由 $x(n)\longleftrightarrow X(Z) = log(1+aZ^{-1})$ 给出
根据性质,我们可以写成
$nx(n)\longleftrightarrow -Z\frac{dx(Z)}{dz}$
$= -Z[\frac{-aZ^{-2}}{1+aZ^{-1}}]$
$= (aZ^{-1})/(1+aZ^{-1})$
$= 1-1/(1+aZ^{-1})$
$nx(n) = \delta(n)-(-a)^nu(n)$
$\Rightarrow x(n) = 1/n[\delta(n)-(-a)^nu(n)]$
时间乘法
它给出了在离散信号级别发生乘法时信号 Z 域的变化。
$x_1(n).x_2(n)\longleftrightarrow(\frac{1}{2\Pi j})[X1(Z)*X2(Z)]$
时间共轭
这描绘了 Z 域中共轭离散信号的表示。
$X^*(n)\longleftrightarrow X^*(Z^*)$
