统计 - 指数分布

指数分布或负指数分布表示描述泊松过程中事件之间时间的概率分布。在泊松过程中，事件以恒定的平均速率连续且独立地发生。指数分布是伽玛分布的一个特例。

指数分布

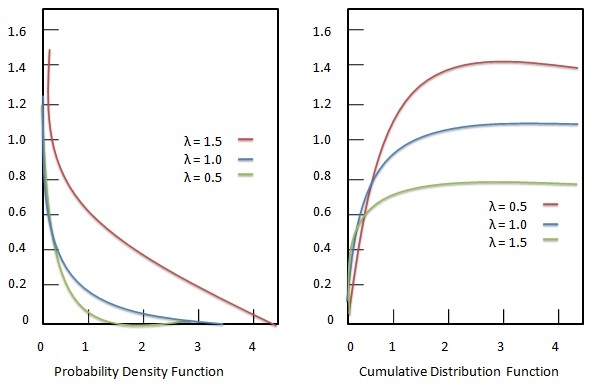
概率密度函数

指数分布的概率密度函数如下：

公式

${ f(x; \lambda ) = } $ $ \begin {cases} \lambda e^{-\lambda x}, & \text{if $x \ge 0 $} \\[7pt] 0, & \文本{if $x \lt 0 $} \end{cases} $

其中 -

  • ${\lambda}$ = 速率参数。

  • ${x}$ = 随机变量。

累积分布函数

指数分布的累积分布函数如下：

公式

${ F(x; \lambda) = }$ $ \begin {cases} 1- e^{-\lambda x}, & \text{if $x \ge 0 $} \\[7pt] 0, & \文本{if $x \lt 0 $} \end{cases} $

其中 -

  • ${\lambda}$ = 速率参数。

  • ${x}$ = 随机变量。