统计 - 正态分布

正态分布是数据集的一种排列，其中大多数值聚集在范围的中间，其余值对称地向任一极端逐渐减小。身高是遵循正态分布模式的一个简单例子：大多数人的身高处于平均水平，高于平均身高和低于平均身高的人数相当相等，只有极少数（但仍大致相当）的人数要么是极端身高，要么是身高低于平均身高。高或极矮。这是正态分布曲线的示例：

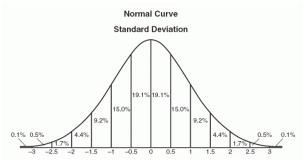
正态分布的图形表示有时被称为钟形曲线，因为它的形状呈喇叭形。精确的形状可能会根据人口的分布而变化，但峰值始终位于中间，并且曲线始终是对称的。在正态分布中，均值众数和中位数都是相同的。

公式

${y = \frac{1}{\sqrt {2 \pi}}e^{\frac{-(x - \mu)^2}{2 \sigma}} }$

其中 -

${\mu}$ = 平均值
${\sigma}$ = 标准差
${\pi \约3.14159}$
${e \约2.71828}$

例子

问题陈述：

对每日出行时间的调查得出以下结果（以分钟为单位）：

平均值为 38.8 分钟，标准差为 11.4 分钟。将值转换为 z 分数并准备正态分布图。

解决方案：

我们一直使用的 z 分数公式：

${z = \frac{x - \mu}{\sigma} }$

其中 -

${z}$ =“z 分数”（标准分数）
${x}$ = 要标准化的值
${\mu}$ = 平均值
${\sigma}$ = 标准差

转换 26：

首先减去平均值：26-38.8 = -12.8，

然后除以标准差：-12.8/11.4 = -1.12

所以 26 是 -1.12 与平均值的标准差

这是前三个转换。

原值	计算	标准分数（z 分数）
26	(26-38.8) / 11.4 =	-1.12
33	(33-38.8) / 11.4 =	-0.51
65	(65-38.8) / 11.4 =	-2.30
...	...	...

在这里，它们以图形方式表示：